Два способа создания объектов PivotCache и PivotTable

Я уже говорил, что объекты PivotCache и PivotTable можно создавать несколькими способами, и рассмотрел методы, используемые в этих способах. Теперь пришла пора привести соответствующие процедуры, решающие эти задачи. Я приведу две процедуры, в каждой из которых создаются оба эти объекты, но в каждой из них это делается по-разному. Вот код первой из этих процедур:

Public Sub CreatePivotCacheAndTable() 'Создание объекта PivotCache 'и на его основе - объекта PivotTable 'при заполнении данными используются 'свойства объекта: Connection,CommandText,CommandType Dim myCache As PivotCache Dim DbDir As String, DbPath As String DbDir = ThisWorkbook.Path DbPath = DbDir & "\dbPP2000.mdb"

Set myCache = ThisWorkbook.PivotCaches.Add(xlExternal) With myCache .Connection = "OLEDB; Provider=Microsoft.jet.oledb.4.0;" & _ "Data Source=" & DbPath .CommandType = xlCmdSql .CommandText = _ "SELECT Заказано.НазваниеКниги, Заказано.Стоимость, " & _ "Заказано.Количество, " & "Заказы.Заказчик, Заказы.Сотрудник, " & _ "Заказы.ДатаЗаказа" & Chr(13) & "" & Chr(10) & _ "FROM `C:\!O2000\DsCd\Ch18\dbPP2000`.Заказано Заказано, " & _ "`C:\!O2000\DsCd\Ch18\dbPP2000`.Заказы Заказы" & _ Chr(13) & "" & Chr(10) & _ "WHERE Заказано.КодЗаказа = Заказы.КодЗаказа" 'Создать отчет сводной таблицы With ThisWorkbook.Worksheets("Лист1") .Activate If .PivotTables.Count > 0 Then 'Очистить область сводной таблицы ClearRegion End If End With .CreatePivotTable TableDestination:=Range("A3"), _ TableName:="Анализ продаж"

End With End Sub

Обратите внимание, как создается объект PivotCache, - вначале он добавляется в коллекцию методом Add, но при этом объект не связан еще ни с каким источником данных и, следовательно, данных не содержит. На следующем этапе при заполнении свойств этого объекта - Connection, CommandType и CommandText - осуществляется связь с источником данных и выполняется команда, задающая запрос на получение данных. Соответствующий участок текста процедуры подсвечен.

Так кэш становится заполненным. После этого, к нему можно привязать и отчет сводной таблицы. В данном варианте для построения объекта PivotTable используется метод CreatePivotTable объекта PivotCache.

Заметьте, нельзя размещать сводную таблицу в области уже занятой другой сводной таблицей. По этой причине в процедуре проводится соответствующая проверка и область очищается, если она была занята. Приведу текст вызываемой процедуры ClearRegion:

Public Sub ClearRegion() Dim myr As Range Set myr = ActiveSheet.UsedRange myr.Clear End Sub

Надеюсь, она не требует особых пояснений. Напомню лишь, что свойство UsedRange возвращает всю область, занятую на рабочем листе. Эта область и очищается.

Давайте рассмотрим теперь другой способ создания объектов PivotCache и PivotTable. Приведу код процедуры для этого варианта:

Public Sub CreatePivotCacheAndTableWithADO() 'Создание объекта PivotCache 'и на его основе - объекта PivotTable 'Связь с базой данных осуществляется с использованием 'объектов ADO: Connection,Command,Recordset 'Объект Recordset является основой для построения кэша Dim myCache As PivotCache 'Соединение с базой данных и получение набора записей CreateRecordset Set myCache = ThisWorkbook.PivotCaches.Add(xlExternal) With myCache Set .Recordset = Rst1 'Создать отчет сводной таблицы With ThisWorkbook.Worksheets("Лист1") .Activate If .PivotTables.Count > 0 Then 'Очистить область сводной таблицы ClearRegion End If .PivotTables.Add PivotCache:=myCache, _ TableDestination:=Range("A3"), _ TableName:="Анализ продаж" End With End With End Sub

В этом варианте построения кэша сводной таблицы за доставку данных от источника данных в программу отвечают хорошо нам знакомые объекты ADO. Этот вариант имеет несомненные достоинства, поскольку объекты ADO обеспечивают эффективную доставку данных и, что не менее важно, способны получать данные из самых разнообразных источников данных, которые теперь можно использовать для построения сводных таблиц.

Работа с объектами ADO заканчивается построением объекта Recordset, задающего набор записей. Теперь остается ссылку на этот объект сделать значением одноименного свойства объекта PivotCache.

Так кэш становится заполненным. После этого, к нему можно привязать и отчет сводной таблицы. В данном варианте для построения объекта PivotTable используется метод Add коллекции PivotTables.

Чтобы закончить рассмотрение, остается привести текст вызываемых процедур CreateConnection и CreateRecordset:

Public Sub CreateConnection() 'Создание соединения с тестовой базой данных Access Dim strConnStr As String If Con1.State = adStateOpen Then Con1.Close 'закрыть соединение 'Конфигурирование соединения Con1 Con1.Provider = "Microsoft.jet.oledb.4.0" Con1.ConnectionString = "Data Source=c:\!O2000\DsCd\Ch14\dbPP2000.mdb" Con1.CursorLocation = adUseClient 'Открытие соединения Con1.Open End Sub



Public Sub CreateRecordset() 'Связывание с базой данных Access ' получение набора записей Dim strSQL1 As String 'Задание SQL оператора strSQL1 = _ "SELECT Заказано.НазваниеКниги, Заказано.Стоимость, " & _ "Заказано.Количество, " & "Заказы.Заказчик, Заказы.Сотрудник, " & _ "Заказы.ДатаЗаказа" & Chr(13) & "" & Chr(10) & _ "FROM `C:\!O2000\DsCd\Ch18\dbPP2000`.Заказано Заказано, " & _ "`C:\!O2000\DsCd\Ch18\dbPP2000`.Заказы Заказы" & _ Chr(13) & "" & Chr(10) & _ "WHERE Заказано.КодЗаказа = Заказы.КодЗаказа" CreateConnection 'задание свойств объекта Command Cmd1.ActiveConnection = Con1 Cmd1.CommandText = strSQL1 Cmd1.CommandType = adCmdText Cmd1.Prepared = True

'вызов команды на исполнение методом Execute Set Rst1 = Cmd1.Execute End Sub

Процедуры CreateConnection и CreateRecordset нам хорошо знакомы, - их аналоги уже появлялись в главе 15 при рассмотрении объектов ADO. При работе с ними, как и ранее, используются глобальные объекты - Con1, Cmd1, Rst1.

Функция ЛИНЕЙН

В общем случае решает задачу линейной множественной регрессии, вычисляя по методу наименьших квадратов вектор оценок параметров. Используется описанная нами выше модель:

Y = X*a + E

Синтаксис вызова этой функции:

ЛИНЕЙН (Известные_значения_Y; Известные_значения_X; Конст; Статистика)

Параметры функции имеют следующий смысл:

Известные_значения_Y - задает вектор измерений.Известные_значения_X - в общем случае матрица значений наблюдаемых параметров. Если речь идет о временном тренде, то элементы X задают моменты времени, в которые проводились измерения. Можно опустить X, если значения элементов составляют последовательность 1, 2, 3 и т. д.Булев параметр "Конст" равен Истина (True), если в линейной записи модели присутствует дополнительно свободный член b, не входящий в вектор параметров a.Булев параметр "Статистика" равен Истина (True), если наряду с оценками параметров вычисляются и статистические характеристики.Результат вычислений этой функции - массив, в общем случае состоящий из 5 строк и n+1 столбцов, где n - это размерность вектора искомых параметров a. an,    an-1, …  a1,  b?n,    ?n-1, …  ?1,  ?bR*R,   ?YF,             dfSsreg, SsresidВ первой строке идут оценки параметров a и свободного члена b. Оценки идут в обратном порядке, начиная с an. Они и определяют линию регрессии, позволяя рассчитать прогнозируемое значение Y в любой точке, где заданы значения наблюдаемых параметров.В следующей строке идут среднеквадратические отклонения этих оценок. Выше мы показали, как вычислить полную корреляционную матрицу оценок. Среднеквадратические отклонения являются диагональными элементами этой матрицы. Точнее, на диагонали стоят их квадраты - дисперсии DI = ?I * ?I. Значения ?I позволяют построить доверительный интервал для соответствующих оценок и вынести суждение об их значимости в линейной модели. Как вычисляются эти значения в Excel, нам осталось непонятно, так как алгоритм не описан. Можно лишь заметить, что применяемый алгоритм не всегда корректен с позиций классической математической статистики. Приведем пример. Пусть оцениваются, как часто бывает, два параметра a и b (Y = at +b). Пусть выполнены всего два измерения - Y1 и Y2. Тогда, каковы ни были ошибки в измерениях, линия регрессии пройдет через две наблюденные точки. Excel скажет, что оши

"µ бок в оценках параметров нет, и выдаст значения ?1 и ?2 , равные 0, хотя ясно, что это не так.Коэффициент детерминации R2 имеет значение в интервале от 0 до 1 и позволяет оценить, насколько хорошо сглаживаются измеренные значения линией регрессии. Он равен 1, если линия регрессии проходит через все измеренные точки. При этом можно полагать, что есть строгая функциональная зависимость между измеряемым значением Y и параметрами ai. Предыдущий пример показывает, что недостаточное количество измерений может приводить к такому же результату. Поэтому и к этому параметру надо относиться с осторожностью. Вычисляется коэффициент детерминации по формуле:

R2 = Dreg / D

и представляет отношение дисперсии, объясняемой регрессией, к общей дисперсии. О смысле этих терминов мы скажем чуть ниже.

Мы и так увлеклись понятиями математической статистики, потому не будем говорить о том, что означают и как используются параметры ?Y, F и число степеней свободы df.Последние два значения - Ssreg и Ssresid задают дисперсию, объясняемую регрессией, и остаточную дисперсию, представляющую разность между общей дисперсией и Dreg. Обе дисперсии вычисляются "обычным" способом:



D = (YI - E)2 ; Dreg = (YI - E)2 ,

где E - среднее значение измеренных значений, а YI - сглаженные значения, вычисленные из уравнения регрессии.

Мы подробно рассказали о "главной" для решения задач прогнозирования функции ЛИНЕЙН. Она позволяет построить уравнение регрессии, как для временных рядов, так и в общем случае линейной множественной регрессии, когда наблюдается несколько параметров.

Функция ТЕНДЕНЦИЯ и другие функции, используемые для прогноза

В основе всех других функций Excel, используемых для прогноза и регрессионного анализа лежит функция ЛИНЕЙН. Так, если уравнение регрессии уже построено, вычислить значение в новой точке нетрудно. Функция ТЕНДЕНЦИЯ решает эту простую задачу. Она неявно вызывает функцию ЛИНЕЙН и, используя полученные оценки параметров, вычисляет прогнозируемые значения в новых точках. Обращение к ней имеет вид:

ТЕНДЕНЦИЯ(Известные_Y, Известные_X, Новые_значения_X, Конст)

Здесь появился один новый параметр, задающий в общем случае матрицу новых значений X. Все остальные параметры имеют тот же смысл, что и в функции ЛИНЕЙН. В результате возвращается вектор прогнозных значений Y, вычисленный в точках, заданных матрицей новых значений X. Каждая ее строка задает одну точку.

Функция ПРЕДСКАЗ - частный случай функции ТЕНДЕНЦИЯ - используется в линейной модели с двумя параметрами, когда уравнение регрессии имеет вид:

y = a*x + b

В этом случае Y и X представляют одномерные массивы данных. Вызов функции таков:

ПРЕДСКАЗ( x; Известные_Y; Известные_X)

Здесь x - точка, для которой строится прогноз.

Мы говорили о возможности построения нелинейного уравнения регрессии, которое простым преобразованием сводится к задаче линейной регрессии. Такое преобразование и осуществляет функция ЛГРФПРБЛ. Формально здесь используется нелинейная модель:

y = b* a1x1 * a2x2 * … * amxm

Простым логарифмированием модель сводится к линейной.

ln(y) = x1* ln(a1) + x2*ln(a2) + … + xm*ln(am) + b

Функция ЛГРФПРБЛ имеет те же параметры, что и функция ЛИНЕЙН. Обращение к ней:

ЛГРФПРБЛ (Известные_значения_Y; Известные_значения_X; Конст; Статистика)

Как работает эта функция, совершенно ясно: она вызывает функцию ЛИНЕЙН, подавая ей на вход не сами измерения Y, а их логарифмы. Полученные оценки достаточно подвергнуть обратному преобразованию - взять экспоненту, и задача решена. Так строится нелинейное уравнение регрессии. Этот нехитрый прием позволяет самому строить новые модели нелинейной регрессии.

Последняя из стандартных функций этого семейства - РОСТ - непосредственно вычисляет значения прогноза в новых точках, используя результаты вызова функции ЛГРФПРБЛ. РОСТ связана с функцией ЛГРФПРБЛ, как ТЕНДЕНЦИЯ связана с ЛИНЕЙН. Обращение к функции имеет вид:

РОСТ(Известные_Y, Известные_X, Новые_значения_X, Конст)

Инструментальная панель "Сводные таблицы"

В процессе создания сводной таблицы по умолчанию включается инструментальная панель "Сводные таблицы". Ее, конечно, при желании можно отключить, но, как правило, она всегда включена, поскольку позволяет выполнять различные операции над сводной таблицей.

Вид инструментальной панели показан на предшествующих рисунках, например, на рис. 8.15. Как я уже говорил, в ней можно выделить две части - в одной из них расположен набор инструментальных кнопок, задающих те или иные функции, во второй - набор полей, доступных при формировании структуры сводной таблицы. Давайте рассмотрим более подробно, что можно делать с помощью кнопок инструментальной панели:

- Эта кнопка позволяет задать форматирование сводной таблицы. Можно выбрать формат из списка, содержащего два десятка возможных форматов. - Задает построение сводной диаграммы. - Вызывает Мастера сводных таблиц, позволяя вернуться к процессу построения таблицы с использованием Мастера. - две кнопки, позволяющие скрыть и показать детали. Особенно полезны при работе с полями, допускающими группировку. Но могут применяться и к большинству других полей. - позволяет обновить данные сводной таблицы, получив их из источника данных. - позволяет задать параметры поля. Для вычислимых полей можно задать соответствующую функцию вычислений. - кнопка для скрытия полей. - первая кнопка, расположенная на панели. При ее нажатии открывается меню, пункты которого выполняют практически все задачи, что и перечисленные выше кнопки, но кроме этого в меню есть и дополнительные возможности, например, можно установить дополнительные свойства сводной таблицы, задав те или иные ее параметры.

Кубы OLAP, сводные таблицы и анализ данных

Прекрасно, когда все необходимые данные хранятся в одной базе данных. Однако для удобной работы с ними этого мало. Данных много, они разбросаны по разным таблицам, - все это не дает возможности их сопоставить, оценить, визуализировать. Поэтому, прежде чем начать серьезный анализ, данные надо представить в удобной форме.

Одно из самых эффективных средств компактного представления данных - сводные таблицы. Эти таблицы являются одним из самых мощных и самых удобных средств анализа данных. Благодаря группировке данных, сводная таблица может представлять большой объем данных в чрезвычайно компактной форме, поддающейся визуализации. С другой стороны, эта таблица при необходимости раскрывается совершенно естественным образом, позволяя получить информацию с нужной степенью подробности. Удивительно, что дать точное определение сводной таблицы достаточно сложно, но работать с ней легко и просто, никаких особых затруднений не возникает даже у пользователей, не обладающих высокой квалификацией. Пожалуй, ни одно из средств Excel, которое будет рассмотрено в этой главе, не обладает столь интуитивно понятным интерфейсом, как сводные таблицы.

Метод экспоненциального сглаживания

В модели устойчивого спроса методы прогноза основаны на скользящем среднем, где вычисляется средневзвешенное значение по результатам предыдущих измерений. Весь вопрос в том, какой временной интервал учитывать и какие веса приписывать данным. Один из простых и лучших методов - экспоненциальное сглаживание, описываемое соотношением:

Pt =

St + (1- )Pt-1

где St - фактический спрос в момент времени t, а Pt - его оценка, экстраполируемая на будущее. Формула показывает, что оценка является взвешенной суммой последнего полученного значения спроса и предыдущей оценки. Параметром метода, устанавливаемым эмпирически, является весовой коэффициент

. Чем меньше , тем большее значение придается прошлым данным. Если же большего доверия заслуживают последние данные, следует увеличивать. Рекомендуемые значения обычно выбираются из интервала 0.1-0.5.

Метод Чоу адаптивного прогнозирования позволяет подбирать

в процессе прогноза. Его суть состоит в том, чтобы одновременно вести три прогноза с разными значениями , например 0.1, 0.15 и 0.2. Если реальный спрос ближе к одной из границ, скажем, верхней, система перестраивается, и новыми значениями будут 0.15, 0.2 и 0.25.

Методы краткосрочного прогноза

Применяемые при краткосрочном прогнозе методы основываются на разных моделях поведения спроса. Наиболее часто используются модели:

устойчивого (постоянного) спроса;линейно изменяющегося спроса (возрастающего или убывающего);сезонного спроса;комбинации этих моделей.

Методы прогнозирования

Сводные таблицы позволяют анализировать прошлое и настоящее. Прогнозирование - это способ заглянуть в будущее. Любая направленная деятельность предполагает построение прогноза параметров, определяющих эту деятельность. Есть два пути прогнозирования. Первый - построить модель поведения исследуемого параметра, основанную на причинно-следственных связях, изучении законов его поведения. Так, довольно просто описать траекторию полета ракеты, подчиняющуюся законам небесной механики. Траекторию управляемого пилотом самолета описать труднее. Еще сложнее описать "траекторию" спроса на тот или иной продукт, поскольку она определяется действиями большого числа "пилотов", которые в любой момент могут начать или перестать покупать фирменный продукт.

Второй путь - статистическое прогнозирование, позволяет, не вдаваясь в механику движения, предсказать будущее поведение, анализируя полученную статистику поведения в прошлом. Статистическое прогнозирование - неотъемлемый атрибут экономической деятельности любого масштаба. Подобный прогноз может быть краткосрочным или среднесрочным. В первом случае прогноз базируется на данных за короткий период времени (например, месяц) и строится на один-два момента вперед. Такой прогноз обычно должен быть оперативным и непрерывным. Среднесрочный прогноз определяет поведение в отдаленном будущем, скажем, на год вперед. Он требует больше данных и специальных методов, отличных от методов краткосрочного прогноза.

О методах прогноза написано много. В документации можно найти обширный список литературы, использованной при построении стандартных процедур. Мы пользовались другими, доступными для нас источниками, и позволим себе без подробных обоснований привести несколько методов. О регрессионном анализе и оценках по методу наименьших квадратов можно прочитать в любом хорошем учебнике по математической статистике. Замечу, что те, кому экскурс в разделы статистики покажется утомительным, могут без особого ущерба пропустить его, и перейти к чтению разделов, где непосредственно рассматриваются соответствующие средства Excel.

Многомерные (OLAP) источники данных

Интерес к кубам OLAP как к одному из ключевых источников данных в последнее время резко возрос. И этому есть понятные объяснения. Сводные таблицы являются одним из основных инструментов анализа данных при работе над документами, как на локальных компьютерах, так и при работе в интрасетях. Эффективность работы со сводными таблицами возрастает, когда источником данных является куб OLAP. Это особенно заметно в тех случаях, когда приходится работать с большими объемами данных. Основная причина в том, что между представлением данных в сводных таблицах и кубах OLAP есть большое сходство. Поэтому большую часть работы по требуемой структуризации данных берут на себя серверы OLAP. Поскольку многие пользователи могут работать с одним и тем же представлением данных, заложенным в кубе OLAP, то сервер единожды выполняет работу, результаты которой используются многократно. Другое достоинство состоит в том, что передавать каждому пользователю можно уже агрегированные данные, что существенно снижает нагрузку на объем передаваемых данных в сети и повышает общую эффективность работы.

Сам термин OLAP означает On-Line Analytical Processing и отражает тот факт, что сервер, хранящий базы данных OLAP, выполняет определенную аналитическую обработку. Часто в термин OLAP вкладывают и другой смысл, отражающий многомерность структуры хранимых данных. Так что, когда говорят о многомерных хранилищах данных, неявно предполагают, что речь идет о базах данных OLAP. Первичной структурой в этих базах является многомерный куб - гиперкуб. Оси этого куба, как и положено, называются измерениями. С каждой точкой в пространстве этого куба связаны данные. Важной особенностью OLAP-куба является то, что на каждом измерении можно задать иерархию, определяющую способ группирования или классификации элементов, принадлежащих данному измерению. Например, одним из измерений куба, хранящего данные о продажах, может быть измерение "Заказчики", на котором естественным образом можно задать иерархию, определяющую географическое распределение заказчиков по континентам, страна м, регионам, городам. На одном измерении можно задать несколько иерархий. Например, тех же заказчиков можно сгруппировать по профессиональным признакам. Кубы OLAP идеально приспособлены для проведения анализа "в глубину". Так пользователь вначале может проанализировать объем заказов по странам. Заметьте, суммарное число заказчиков может быть очень большим и измеряться десятками тысяч, в то же время число стран будет измеряться единицами, так что объем передаваемой информации будет малым. При необходимости пользователь может для той или иной страны проанализировать распределение по регионам, для некоторых выбранных регионов - по городам, так можно дойти и до конкретного заказчика и проанализировать сделанные им заказы. Внутри куба OLAP можно производить и итоговые вычисления, применяя, например, функции суммирования данных, вычисления среднего, нахождения максимума и другие.

Отметим, что кубы OLAP могут существовать и вне базы OLAP, как отдельные файлы. В этом случае они могут использоваться и в режиме Offline даже при работе вне сети.

Объект PivotCache и коллекция PivotCaches

Коллекция PivotCaches возвращается при вызове одноименного свойства объекта Workbook. Как и большинство коллекций, она устроена достаточно просто. У нее типичные для коллекций свойства: Application, Count, Creator, Parent. Методы также классические - Item и Add. Из всего этого набора заслуживает рассмотрения только метод Add, позволяющий создать новый объект. Вот его синтаксис:

Expression.Add(SourceType, SourceData)

Здесь Expression - выражение, возвращающее объект класса PivotCaches. Аргументы метода имеют следующий смысл:

SourceType - задает тип источника данных. Значение аргумента может быть одной из следующих четырех констант: xlCosolidation, xlDatabase, xlExternal, xlPivotTable. Каждая из этих констант задает один из четырех возможных типов, которые уже обсуждались, когда речь шла о первом шаге работы Мастера сводных таблиц, смотри, например, рис. 8.1.SourceData - возможный аргумент, который не следует задавать, если первый аргумент имеет значения xlExternal, то есть задает внешний источник данных. Для остальных трех значений первого аргумента параметр SourceData определяет источник данных. Тип этого аргумента, естественно зависит от значения первого аргумента. Так, если первый аргумент определяет базу данных Excel, то аргумент задается объектом Range, определяющим эту базу. Если речь идет о диапазонах консолидации, то аргумент задается массивом из объектов Range. В случае, когда речь идет о другой сводной таблице, как источнике данных, то аргумент задается строкой текста, представляющей имя сводной таблицы.

Конечно, более всего, для нас интересен случай, когда источником построения сводной таблицы является база данных. Понятно, что в этом случае метод Add определяет пустой объект PivotCache, еще не заполненный данными, поскольку второй параметр при выполнении метода не задается и источник данных, следовательно, не определен. Как же происходит заполнение объекта PivotCache данными в этом случае? Ответ прост - при установлении свойств объекта. Ситуация во многом напоминает работу с объектом Command из библиотеки ADO. У объекта PivotCache имеются свойства - Connection, CommandType, CommandText, аналогичные одноименным свойствам объекта Command.

Давайте перейдем к рассмотрению свойств и методов объекта PivotCache.

Объект PivotTable и коллекция PivotTables

Если коллекция PivotCaches связана с рабочей книгой, то коллекция PivotTables связана с отдельным листом этой книги. Коллекция PivotTables возвращается при вызове одноименного свойства объекта Worksheet. Обе коллекции устроены одинаково и имеют один и тот же набор свойств и методов. У коллекции PivotTables имеются следующие свойства: Application, Count, Creator, Parent. У нее есть также два метода - Item и Add. Из всего этого набора заслуживает рассмотрения только метод Add, позволяющий создать новый объект. Вот его синтаксис:

Function Add(PivotCache As PivotCache, TableDestination, [TableName], [ReadData]) As PivotTable

Чуть выше я рассматривал, как основной способ создания объектов PivotTable, вызов метода CreatePivotTable объекта PivotCache. Я называл этот способ основным по той причине, что создание кэша не является самоцелью, - это не самостоятельный объект. Всегда он создается для того, чтобы связать с ним отчет сводной таблицы - объект PivotTable. Поэтому разумно, создав объект PivotCache тут же вызвать его метод CreatePivotTable, чтобы создать и объект PivotTable.

Тем не менее, для создания объекта PivotTable есть возможность использовать метод Add коллекции PivotTables. Он выполняет ту же работу, что и метод CreatePivotTable, и имеет тот же набор аргументов. Дополнительно, в качестве первого аргумента, естественно, указывается объект PivotCache, на основе которого создается объект PivotTable.

Чуть позже я приведу примеры, где будет показано применение обоих способов создания объекта PivotTable.

Оптимизация и анализ "Что, если ...?"

Средства оптимизации - мощные инструменты, используемые в анализе "Что, если ...?". Рассмотрим вначале то, что попроще. "Подбор Параметра" позволяет для функции одного параметра F(a) подобрать, если можно, такое значение параметра a^, что функция в этой точке будет иметь заранее заданное значение F* = F(a^). Наш менеджер, найдя наилучший вариант сценария, спросил себя: "Что, если слегка увеличить тираж? Увеличу ли я за счет этого доход до 200 000?" Чтобы ответить на эти вопросы, он выбрал в меню "Сервис" пункт "Подбор параметра". В появившемся окне он задал доход как целевую функцию, 200000 - как желаемое значение дохода, Тираж - как параметр (изменяемую ячейку), значение которого нужно подобрать так, чтобы достичь заданной величины дохода. Но сделать этого невозможно. В такой постановке у задачи решения нет, о чем и было ему сообщено. Менеджеру пришлось умерить свои аппетиты: он повторно вызвал "Подбор параметра

"µ ", задав теперь значение дохода, равное 180000. Теперь решение удалось найти. Оно достигается при тираже, равном 10900. Менеджер округлил значение тиража до 10500, что принесло увеличение дохода еще на 10000. На этом менеджер и остановился. Найденное им решение практически оптимально.

Подбор параметра можно осуществлять и программно. Для этого следует вызвать метод GoalSeek объекта Range. Вызывает этот метод объект Range, задающий целевую функцию. Синтаксис метода:

Function GoalSeek(Goal, ChangingCell As Range) As Boolean

Параметр Goal задает значение целевой функции, а параметр ChangingCel - изменяемую ячейку (параметр целевой функции), значение которой будет изменяться, в попытке достичь заданного значения целевой функции. Функция GoalSeek возвращает True в случае успеха и False в противном случае. Вот пример процедуры, вызывающей эту функцию:

Sub ПодборПараметра() Dim Res As Boolean 'Доход - имя целевой ячейки - H49, вычисляющей доход Res = Range("H49").GoalSeek(Goal:=200000, ChangingCell:=Range("J37")) If Res Then Доход = 200000 Else 'Восстанавливаем нормальные значения в ячейках ActiveSheet.Scenarios(3).Show Res = Range("H49").GoalSeek(Goal:=180000, ChangingCell:=Range("J37")) If Res Then Доход = 180000 End If MsgBox ("Ваш Доход = " & Доход) End Sub

И в заключение этой главы об анализе офисной деятельности и используемых для этого средствах Excel взгляните на окошко, уведомляющее о достигнутом доходе:

Рис. 8.37.  Уведомление о достигнутом доходе

И в заключение этой главы об анализе офисной деятельности и используемых для этого средствах Excel взгляните на окошко, уведомляющее о достигнутом доходе:


Рис. 8.37.  Уведомление о достигнутом доходе

© 2003-2007 INTUIT.ru. Все права защищены.

Построение модели прогноза продаж книг офиса "РР"

Рассмотрим теперь применение этих методов для построения модели прогноза продаж книг офиса "РР". Вернемся к таблице, где представлены данные о продажах в течение последних 10 недель. Менеджера интересует прогноз на последующий месяц, и хотя, как мы убедились, он умеет прогнозировать продажи, используя полученное уравнение регрессии, теперь он хочет воспользоваться стандартными функциями прогноза, которые только что были рассмотрены.

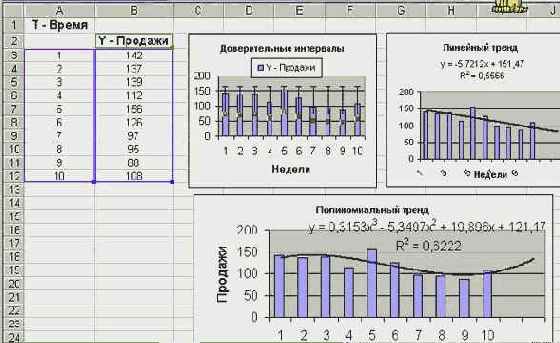
Менеджер начинает работу с визуального анализа данных. Для этой цели он использует возможности визуального представления на диаграмме линии тренда, прогноз значений тренда на требуемый период, возможность задания доверительных интервалов. Эту визуализацию можно сделать как вручную, так и программно. Наш менеджер для таблицы продаж построил три одинаковые диаграммы, на каждой из которых дополнительно вывел:

доверительные интервалы;прямолинейный тренд и некоторые его характеристики;полиномиальный тренд и его характеристики.

увеличить изображение
Рис. 8.28.  Диаграммы, доверительные интервалы и линии тренда

На первой из диаграмм менеджер дополнительно вывел доверительные интервалы шириной в 2? (среднеквадратичное отклонение). Такой интервал с высокой вероятностью накрывает истинное значение. Правда, построенный интервал не отражает динамики изменения данных и, к сожалению менеджера, слишком велик.

На второй диаграмме показан прямолинейный тренд, выведено уравнение регрессии и построен прогноз на ближайшие три недели. Таким образом, здесь в визуальной форме отражены результаты вычислений функций ЛИНЕЙН и ТЕНДЕНЦИЯ. На третьей диаграмме - полиномиальный тренд, где линия регрессии задается кубическим полиномом.

Несколько слов о том, как вручную можно получить диаграммы с трендом и доверительными интервалами. Построив диаграмму, щелкните правой кнопкой в одном из рядов диаграммы и из контекстного меню выберите пункт "Формат рядов данных" и затем вкладку "Y-погрешности". В появившемся окне укажите, отображать ли планки погрешностей, одну или обе, и установите величину погрешности (ее тип, например, стандартное отклонение), количество единиц погрешности. Так визуализируются доверительные интервалы на диаграмме. Для отображения тренда из контекстного меню нужно выбрать пункт "Добавить линии тренда", в появившемся окне - вкладку "Тип" и задать один из 6 возможных типов тренда: линейный, полиномиальный, логарифмический, показательный, экспоненциальный или скользящее среднее. Вкладка "Параметры" позволяет вывести на диаграмму уравнение линии регрессии. Что более важно, тут же можно задать количество интервалов (вперед и назад), для которых будут построены и выведены на график прогнозируемые значения.

Построение OLAP-куба

Excel позволяет по данным внешних источников построить не только сводную таблицу, но и многомерный куб данных - OLAP куб. Цель этого построения - использовать в дальнейшем этот куб, как источник данных для сводной таблицы. При больших объемах данных, используемых при построении сводной таблицы, эффективность работы может быть существенно повышена, если сводная таблица использует OLAP куб.

Работа по построению OLAP куба начинается с построения сводной таблицы. Но в тот момент, когда построен запрос, извлекающий данные из базы данных, можно перейти к построению OLAP куба. Взгляните на рис. 8.7, где показан завершающий шаг построения запроса, - здесь можно включить соответствующий переключатель и перейти к созданию OLAP куба. В примере, где это окно не появлялось, и где запрос создавался непосредственно в Microsoft Query, что показано на рис. 8.10, для построения OLAP куба можно выбрать соответствующий пункт из меню File.

Итак, построение OLAP куба в Excel начинается так же, как и построение сводной таблицы вплоть до момента завершения построения запроса. В этот момент появляется возможность построить OLAP куб по запросу. Давайте продолжим рассмотрение, начиная с этого момента. Предположим, что в окне, показанном на рис. 8.7, я выбрал третий переключатель, запустив, тем самым, на исполнение нового Мастера - Мастера построения OLAP куба. Взгляните, как выглядит первое окно, открываемое этим Мастером:

Рис. 8.19.  Первое информационное окно Мастера построения OLAP куба

В этом информационном окне перечислены достоинства OLAP кубов, есть возможность перейти к подробной справке, которую рекомендую внимательно прочесть на досуге. А мы пока пойдем дальше, следуя за Мастером. На первом шаге своей работы он предлагает задать вычисляемые поля и определить функцию, используемую при вычислениях. Вот как выглядит это окошко:

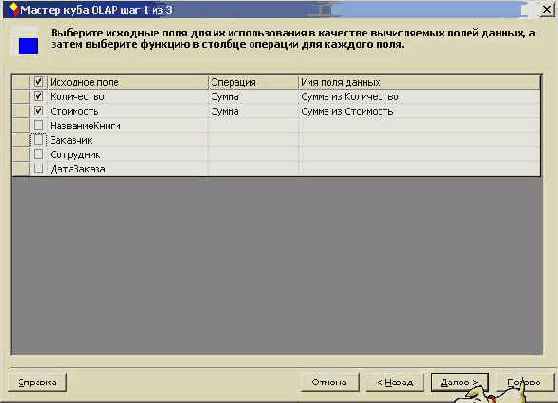
Рис. 8.20.  Окно первого шага Мастера построения OLAP куба

Заметьте, по умолчанию все численные поля являются вычисляемыми, а в качестве функции применяется функция "Сумма". Я оставил предлагаемые установки и перешел к следующему шагу работы. На этом шаге работы Мастер предлагает создать измерения нашего куба:

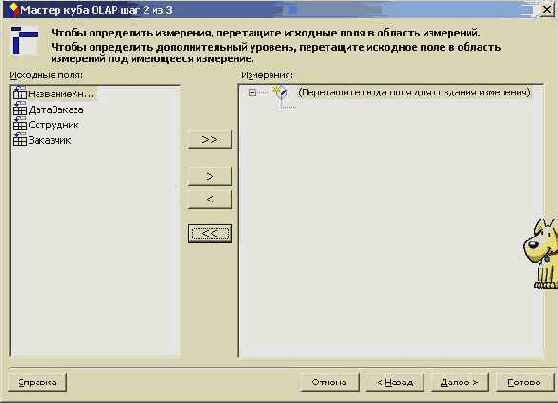
Рис. 8.21.  Создание измерений OLAP куба

Заметьте также, вычисляемые поля стали полями данных. Все оставшиеся поля я перетащил, и они стали измерениями нашего куба. Поле "Дата заказа", имеющее тип даты, автоматически породило иерархию на соответствующем измерении. Понятно, что можно и самому создать иерархию при перетаскивании полей, например, когда речь идет о многократно упоминавшихся полях типа: Страна - Регион - Город. Взгляните на результат создания измерений:

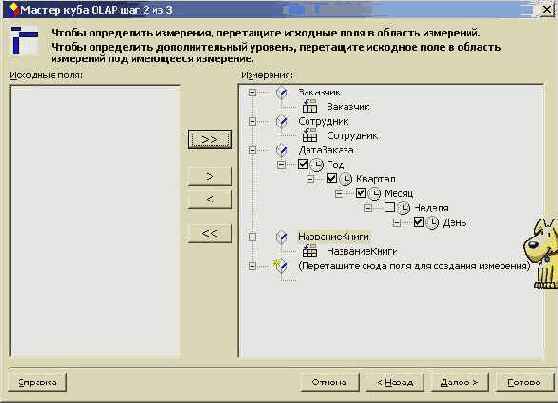
Рис. 8.22.  Результат создания измерений OLAP куба

На заключительном шаге работы Мастер предлагает сохранить OLAP куб. Здесь можно выбрать, сохранить ли только определение куба - файл с уточнением "oqy" или сам куб с данными - файл с уточнением "cub". Сохранение самого куба хотя и требует времени, но обеспечивает более быструю работу со сводной таблицей в дальнейшем при использовании куба.

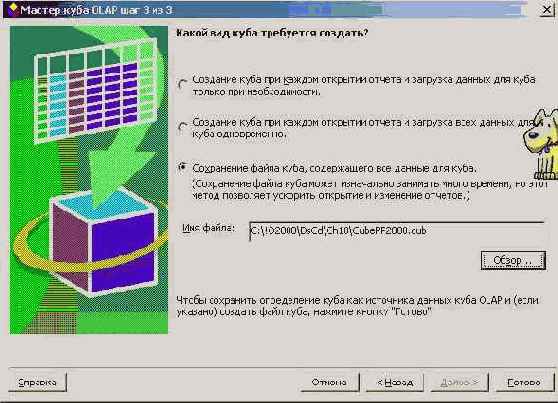
Рис. 8.23.  Сохранение OLAP куба

Я предпочел сохранить сам куб. На этом построение куба завершено. Но чтобы рассказ о нем был завершен, следует привести сводную таблицу, построенную на этом кубе. Опускаю детали, их и так было достаточно, приведу окончательный результат:

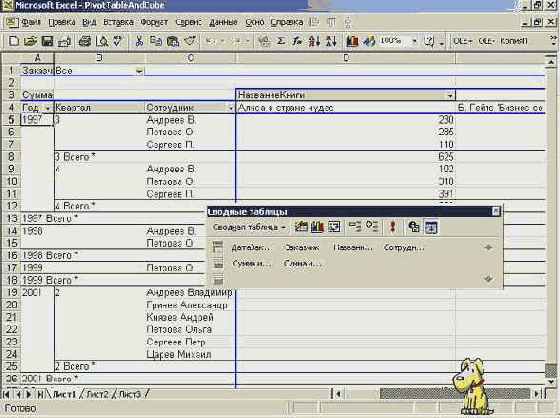
увеличить изображение
Рис. 8.24.  Сводная таблица, созданная на основе OLAP куба

Заметьте, есть некоторые отличия в сводных таблицах, построенных на основе OLAP куба. В частности, удобнее работать с измерениями, имеющими иерархию. В нашем примере это можно заметить при работе с датами.

Построение сводной таблицы вручную

Сводные таблицы обычно строятся вручную специальным инструментом - Мастером сводных таблиц. Сравнительно просто построить эти таблицы и программно. Программист, конечно, должен уметь пользоваться таким инструментом, как Мастер сводных таблиц, хотя главное для него - знание объектной модели сводной таблицы. Причина понятна, - в разрабатываемом программистом офисном приложении не всегда можно требовать от пользователя умение строить самому сводную таблицу и часто эту таблицу надо строить программно, выяснив в диалоге требования пользователя. По сути, надо уметь строить собственного Мастера, который вел бы диалог с пользователем на более понятном языке, подходящем к данной конкретной ситуации.

Программная реализация предполагает знакомство с соответствующими классами объектов. Сама таблица и все ее части являются объектами, классы которых содержат большое количество свойств и методов. Об объектной модели сводной таблицы поговорим чуть позже, а сейчас рассмотрим на конкретном примере построение таблицы с использованием Мастера сводных таблиц. В примере я использую в качестве источника данных уже созданную базу данных офиса "Родная Речь", с которой шла работа в предыдущей главе. Замечу, что эта база данных в офисе используется уже давно, и потому там хранятся сведения о продажах за несколько лет.

При построении сводной таблицы я включу в нее данные, хранящиеся в разных таблицах базы данных. При анализе деятельности меня могут интересовать самые разные вопросы:

Как шли продажи в стоимостном и количественном исчислении за те или иные периоды времени?Какие книги продавались наиболее успешно?Кто из сотрудников офиса оформлял наибольшее число заказов?С кем из заказчиков шла наиболее успешная работа?С какими городами шло наиболее успешное сотрудничество?

Наша сводная таблица должна позволять менеджеру, проводящему анализ отвечать на все эти вопросы. Вся необходимая информация хранится в таблицах: "Заказы", "Заказано", "Заказчики". Поля из этих таблиц и будут использоваться при построении сводной таблицы.

Итак, цель ясна - приступим?

В документе Excel я выбрал рабочий лист, на котором предполагаю поместить сводную таблицу, выбрал ячейку, задающую ее начало. Теперь можно начать работу с Мастером сводных таблиц, для чего в главном меню я выбрал пункт "Данные" и в нем пункт "Сводная таблица. Вот как выглядит первое окно, открываемое Мастером:

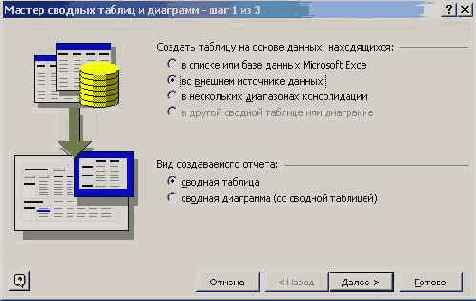
Рис. 8.1.  Первое окно Мастера сводных таблиц и диаграмм

Заметьте, из четырех возможностей задания разных типов источников данных - списков Excel, внешних источников, нескольких диапазонов, другой сводной таблицы - я выбрал внешний источник данных, поскольку, как я уже говорил, буду строить сводную таблицу, используя базу данных Access. Вторая группа переключателей позволяет задать желаемый вид отчета - сводную таблицу или сводную диаграмму, построенную на основе сводной таблицы. Пример с диаграммой приведем чуть позже, а сейчас займемся чисто сводными таблицами. Сделав выбор, остается нажать кнопку "Далее", что заставляет Мастера сделать очередной шаг. Вот окно, открываемое на втором шаге:

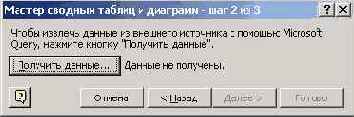
Рис. 8.2.  Окно второго шага Мастера сводных таблиц

Взгляните на результат моей работы:


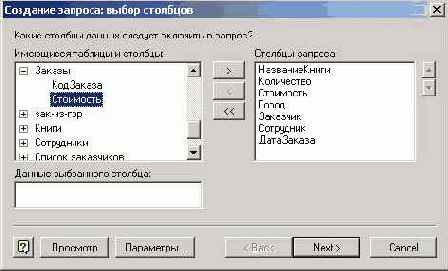
Рис. 8.5.  Выбор полей базы данных для включения их в сводную таблицу

Нажатие кнопки "Next" заставляет Мастера запросов перейти к очередному шагу. Что будет выполняться на следующем шаге, зависит от того, сумеет ли Мастер запросов извлечь требуемые данные из таблиц базы данных. Если проблем у него не возникает, то Мастер запросов предложит создать фильтр для отбираемых данных. Вот как выглядит соответствующее окно в несколько более простой ситуации, когда не включено поле "Город" в число полей, запрашиваемых для построения сводной таблицы.


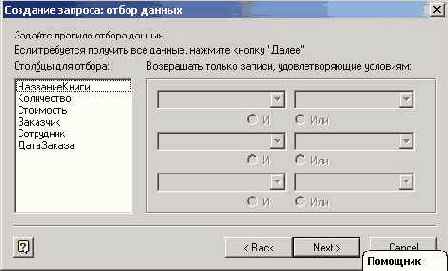
Рис. 8.6.  Запрос на построение фильтров

Окно, следующее за построением фильтров, позволяет задать требуемый порядок сортировки данных. Я не буду приводить его. Взгляните, как выглядит следующее окно, завершающее построение запроса для рассматриваемой ситуации:


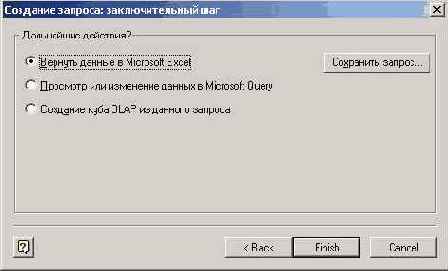
Рис. 8.7.  Завершающий шаг построения запроса

На этом шаге можно, как видите, сохранить запрос, нажав соответствующую командную кнопку. Здесь также следует сделать выбор одной из трех возможностей:

вернуть данные в Excel и возвратиться к очередному шагу работы Мастера сводных таблиц и диаграмм,перейти в Microsoft Query и там продолжить работу над запросом,перейти к построению OLAP куба.

Обычная практика состоит в том, что выбирается первый пункт, и данные возвращаются в Excel. Мы тоже вернемся в Excel, но чуть попозже, а пока рассмотрим исходную ситуацию, когда поле "Город" включено в запрос. Эта ситуация при построении запроса оказалась чуть более сложной, и у Мастера построения запросов возникли некоторые трудности, - он оказался не в состоянии разобраться в связях между таблицами базы данных, и попросил выполнить эту работу вручную, перейдя в Microsoft Query. Вот появляющееся сообщение о возникших у него трудностях:


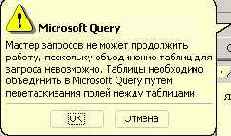
Рис. 8.8.  Сообщение о возникших трудностях у мастера запросов

Заметьте, при работе с моей базой данных я установил все необходимые связи, что видно из рисунка, отображающего схему данных:


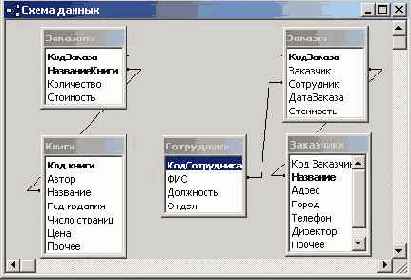
Рис. 8.9.  Схема данных базы "dbPP2000"

Тем не менее, я не отказываюсь помочь Мастеру и выполняю требуемую им работу. Путем перетаскивания полей я добавляю отсутствующую связь между таблицами "Заказчики" и "Заказы". Таблицы связаны общим полем - "Заказчик" в таблице "Заказы", "Название" в таблице "Заказчики". Вот как выглядит окно Мастера запросов, в котором я уже выполнил необходимую работу:


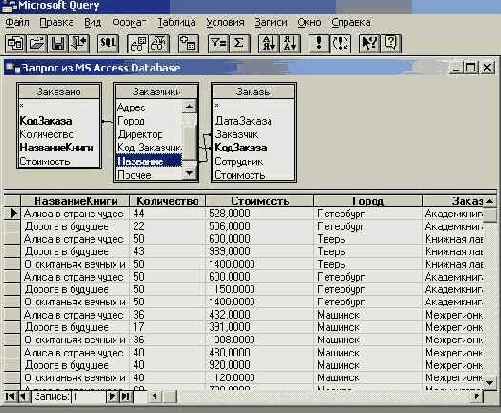
Рис. 8.10.  Установление связей между таблицами

Открывшееся окно Microsoft Query имеет главное меню из многих пунктов и панель с набором инструментальных кнопок. Но я не буду описывать весь спектр возможностей этого инструмента. Нам еще придется работать с ним в дальнейшем. Сейчас же, установив связи между таблицами, и, тем самым, выполнив всю требуемую работу, я просто закрыл это окно, что возвращает нас ко второму шагу Мастера сводных таблиц и диаграмм, но уже в новом состоянии, когда данные для построения сводной таблицы получены:


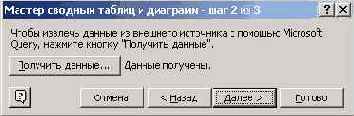
Рис. 8.11.  Новое состояние окна Мастера сводных таблиц на втором шаге

Заметьте, теперь, в отличие от рисунка 8.2, наряду с уведомлением о получении данных стала доступной кнопка "Далее", которую я и нажал для перехода к последнему шагу работы Мастера:


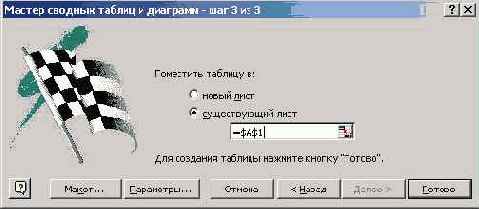
Рис. 8.12.  Заключительный шаг работы Мастера сводных таблиц

На заключительном шаге работы можно указать рабочий лист и ячейку, начиная с которой будет располагаться сводная таблица. Заметьте, наряду с кнопкой "Готово", нажатие которой завершает работу Мастера, в нашем распоряжении есть и другие кнопки, в частности, кнопка "Макет". Вот как выглядит окно макета сводной таблицы:


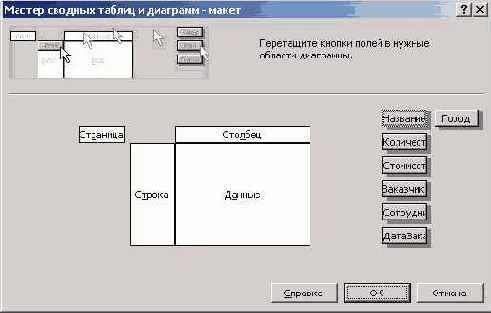
Рис. 8.13.  Макет сводной таблицы

На макете представлена схема сводной таблицы, - четыре области таблицы, озаглавленные соответственно "Страница", "Строка", "Столбец" и "Данные". На макете также представлены поля, отобранные для построения сводной таблицы. Каждое из полей может быть перетащено в одну из областей таблицы. Заметьте, вовсе не обязательно перетаскивать сразу все поля. Как я уже говорил, одно из достоинств сводных таблиц состоит в том, что их структуру можно легко перестраивать в зависимости от целей, которые менеджер, работающий с таблицей, ставит при анализе данных.

Я не стал работать с макетом таблицы, предпочтя окончательную работу по формированию таблицы сделать чуть позже. Поэтому вместо кнопки "Макет" в окне, показанном на рис. 8.10, я нажал кнопку "Готово". В результате Мастер сводных таблиц разместил на выбранном рабочем листе по существу макет сводной таблицы, открыл инструментальную панель с именем "Сводные таблицы", и на этом завершил свою работу. Вот как выглядит рабочий лист Excel по окончании работы Мастера:


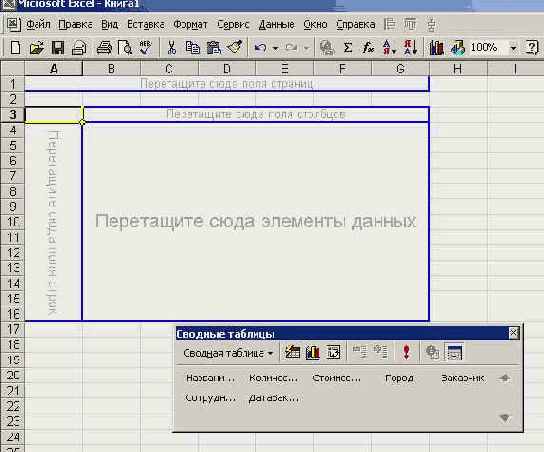
Рис. 8.14.  Рабочий лист с макетом сводной таблицы и инструментальной панелью

Теперь пришла пора заключительного этапа формирования структуры сводной таблицы, - необходимо разумным образом переместить доступные поля в четыре области таблицы. Заметьте, не обязательно перемещать все поля и не обязательно заполнять область страниц. Разумность задания той или иной структуры сводной таблицы определяется целями проводимого анализа, опытом и привычкой.

Я в данном примере размещу все поля и приведу некоторые аргументы в пользу выбранного мной варианта размещения полей:

В область данных я поместил поля "Стоимость" и "Количество". Это, наверное, совершенно естественный выбор, когда речь идет об анализе продаж какого либо товара. Область данных в этом случае отображает данные о продажах в количественном и стоимостном выражении.В область столбцов я поместил поле с названиями книг. По сути, это названия продаваемых товаров.В область строк я поместил два поля - "ДатаЗаказа" и "Сотрудники".В область страниц я также поместил два поля - "Заказчики" и "Город", задающий расположение заказчиков.

Применение сценариев для решения задачи менеджера

Итак, сформулирована задача, в которой имеется результирующая функция, задающая доход. Эта функция зависит от многих параметров. Некоторыми из них можно управлять. Задача, которую должен решить менеджер для оптимизации дохода, заключается в поиске подходящих значений этих параметров. Конечно, можно считать, что наилучшие значения этих параметров менеджер мог бы получить, если бы попытался решать свою задачу как задачу оптимизации. Но здесь не все так просто. Точная формулировка задачи оптимизации потребовала бы дополнительных усилий, трудно было бы сформулировать некоторые ограничения, например, условия накладываемые типографией. Можно отметить и сложность решения оптимизационных задач. Кроме того, часто нет смысла стрелять из пушки по воробьям и искать точное решение в условиях, когда сама модель и ее параметры далеко не точны и отражают лишь суть дела.

В этих типичных условиях сценарии имеют большое практическое значение. Здесь пользователю предоставляется возможность рассмотреть наиболее разумные варианты. А опытный пользователь в своем деле эксперт - всегда знает, где лежит подходящее решение. Поэтому ему достаточно обычно просмотреть несколько возможных вариантов и выбрать наилучший среди них. Варианты, или, как их называют, сценарии, могут быть предложены разными специалистами. Отчет по результатам применения различных сценариев позволяет обосновать принятое решение.

Я специально построил довольно сложную результирующую функцию, по ходу вычисления которой приходится выполнять сложные расчеты, в том числе обращаться к процедурам, написанным на VBA. Вообще результаты принятого решения можно оценивать сразу по нескольким критериям, так что функций, выдающих результат, может быть несколько. Все это не мешает применять сценарии.

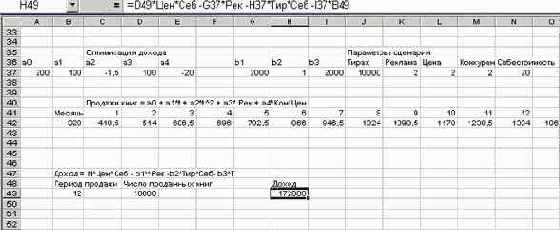
Рассмотрим решение задачи менеджера с применением сценариев. Обращаю внимание, что прежде чем обращаться к сценариям предстоит довольно большая работа по формированию на рабочем листе модели исследуемого процесса. В этой модели нужно определить ту функцию, которая подлежит оптимизации, параметры, которые будут изменяться в сценариях. На нашем примере можно убедиться, что это, возможно, достаточно серьезная работа. Но не буду Вас больше пугать, лучше взгляните, как выглядит рабочий лист, на котором эта работа уже проделана:

увеличить изображение
Рис. 8.31.  Решение задачи менеджера с применением сценариев

Опишем последовательно этапы решения задачи:

На рабочем листе Excel вначале выписаны все параметры, используемые в модели.Затем построена таблица подстановки с данными по продаже книг по месяцам в течение года. Для расчета прогнозируемых значений продаж используется построенное менеджером соотношение, задающее продажи книг. Общий вид его приведен выше. В терминах ячеек Excel эта функция записана в ячейку B42 и имеет вид:

=A37 + B37*A40 +C37*A40*A40 +D37*Рек +E37*Кон*Цен

Эта функция и используется в таблице подстановки, расположенной в ячейках B41:N42.

Значения используемых в расчетах параметров видны на рисунке.

Далее вычисляется период продаж T. В соответствующей ячейке - B49 вызывается пользовательская функция ПериодПродаж:

=ПериодПродаж(C42:N42; Тир)

У нее на входе два параметра. Первый - объект Range, задающий продажи книг, определенные в таблице подстановки на предыдущем этапе; второй - тираж книг. В результате функция возвращает количество месяцев, в течение которых распродан тираж. Если он не распродан в течение года, возвращается число 13. Вот текст этой простой функции:

Public Function ПериодПродаж(Sails As Variant, Tir As Integer) As Integer 'Вычисляет число месяцев, в течение которых распродан тираж. 'Если тираж не распродан в течение года, возвращается число 13 'Параметр Sails задает продажи по месяцам, Tir - объем тиража Sum = 0 For i = 1 To 12 Sum = Sum + Sails.Cells(i) If Sum >= Tir Then Exit For Next i ПериодПродаж = i End FunctionЗатем вычисляется количество проданных книг по формуле:

If T < 13 Then N = Тир Else N = SumNI

где SumNI посчитано заранее вместе с таблицей подстановки. Для реализации данного соотношения в соответствующую ячейку - D49 записана формула:

=ЕСЛИ(B49<13;J37;O42)На следующем шаге в ячейку - H49, задающую доход, я записал формулу, его вычисляющую:

=D49*Цен*Себ -G37*Рек -H37*Тир*Себ -I37*B49

Общую формулу определения дохода я приводил выше.



На этом завершается подготовительный этап работы по формированию на рабочем листе нужной модели. Теперь модель определена, - пора задать сценарии. Вручную это делается так. В меню "Сервис" выбирается пункт "Сценарии", а в открывшемся окне Диспетчера сценариев - нужная кнопка. Для первоначального создания сценариев служит кнопка "Добавить". Вот это окно:


Рис. 8.32.  Окно диспетчера сценариев

В окне добавления сценария указывается его имя, даются ссылки на изменяемые ячейки, устанавливается защита сценария. Вот его вид:


Рис. 8.33.  Добавление сценария



=A37 + B37*A40 +C37*A40*A40 +D37*Рек +E37*Кон*Цен

Эта функция и используется в таблице подстановки, расположенной в ячейках B41:N42.

Значения используемых в расчетах параметров видны на рисунке.

Далее вычисляется период продаж T. В соответствующей ячейке - B49 вызывается пользовательская функция ПериодПродаж:

=ПериодПродаж(C42:N42; Тир)

У нее на входе два параметра. Первый - объект Range, задающий продажи книг, определенные в таблице подстановки на предыдущем этапе; второй - тираж книг. В результате функция возвращает количество месяцев, в течение которых распродан тираж. Если он не распродан в течение года, возвращается число 13. Вот текст этой простой функции:

Public Function ПериодПродаж(Sails As Variant, Tir As Integer) As Integer 'Вычисляет число месяцев, в течение которых распродан тираж. 'Если тираж не распродан в течение года, возвращается число 13 'Параметр Sails задает продажи по месяцам, Tir - объем тиража Sum = 0 For i = 1 To 12 Sum = Sum + Sails.Cells(i) If Sum >= Tir Then Exit For Next i ПериодПродаж = i End FunctionЗатем вычисляется количество проданных книг по формуле:

If T < 13 Then N = Тир Else N = SumNI

где SumNI посчитано заранее вместе с таблицей подстановки. Для реализации данного соотношения в соответствующую ячейку - D49 записана формула:

=ЕСЛИ(B49<13;J37;O42)На следующем шаге в ячейку - H49, задающую доход, я записал формулу, его вычисляющую:

=D49*Цен*Себ -G37*Рек -H37*Тир*Себ -I37*B49

Общую формулу определения дохода я приводил выше.



На этом завершается подготовительный этап работы по формированию на рабочем листе нужной модели. Теперь модель определена, - пора задать сценарии. Вручную это делается так. В меню "Сервис" выбирается пункт "Сценарии", а в открывшемся окне Диспетчера сценариев - нужная кнопка. Для первоначального создания сценариев служит кнопка "Добавить". Вот это окно:


Рис. 8.32.  Окно диспетчера сценариев

В окне добавления сценария указывается его имя, даются ссылки на изменяемые ячейки, устанавливается защита сценария. Вот его вид:


Рис. 8.33.  Добавление сценария

В следующем окне задаются значения изменяемых ячеек, устанавливаемых сценарием:


Рис. 8.34.  Установка значений параметров, заданных сценарием

Последовательно можно задать нужное количество сценариев. Но их можно добавлять в любой момент, изменять возможные значения его параметров. И главное, сценарии можно выполнять, и тогда все соотношения, определенные моделью, будут посчитаны для заданного сценарием набора значений управляющих параметров.

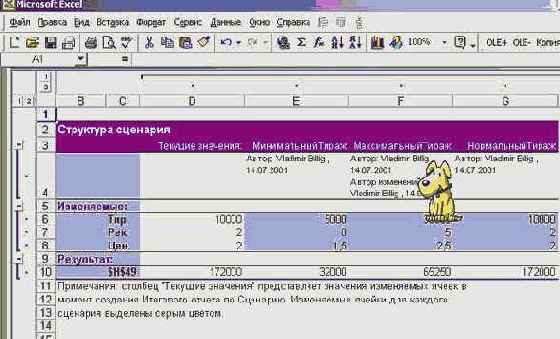
Заключительный шаг при работе со сценариями - подведение итогов. Щелкнув в окне Диспетчера кнопку "Отчет" и выбрав один из двух типов отчета, Вы получите итоговый отчет, позволяющий обосновать принимаемое решение:


увеличить изображение
Рис. 8.35.  Отчет по результатам вычисления сценариев

Кнопки в левом поле сценария позволяют скрыть или развернуть для показа его отдельные части. В примере вся информация о сценариях показана. С содержательной точки зрения главным итогом является обоснование принятого менеджером решения применить сценарий "Нормальный тираж" - он и обеспечивает максимальный выигрыш.

Пример применения функции ЛИНЕЙН в задаче прогнозирования

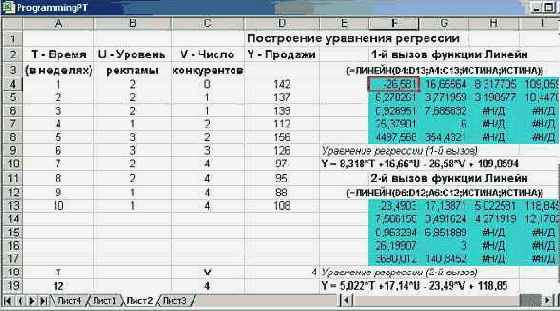
Приведем теперь пример применения функции ЛИНЕЙН. Менеджер офиса "РР" решил построить уравнение, прогнозирующее продажи одной из книг. В его распоряжении были данные по продажам этой книги за последние 10 недель. Агенты офиса фиксировали также уровень рекламы и количество конкурирующих товаров (книг на аналогичную тему). Используя функцию ЛИНЕЙН, менеджер построил уравнение множественной регрессии. Взгляните, как выглядит лист рабочей книги Excel, где размещены данные о продажах и где менеджер построил уравнение регрессии, основываясь на этих данных:

увеличить изображение
Рис. 8.26.  Построение уравнения регрессии по данным продаж

Менеджер построил это уравнение дважды, получив два уравнения - Y1 и Y2, используя выборки измерений разного объема. Этот полезный прием позволяет понять, насколько полученные коэффициенты критичны к измерениям.

Наш менеджер достаточно хорошо разбирается в статистике, поэтому он тщательно проанализировал все данные, возвращаемые функцией ЛИНЕЙН для двух ее вызовов. Обратите внимание, массивы результатов работы функции на рисунке подсвечены. Смысл каждого из результирующих параметров выше уже был пояснен и я не буду на этом останавливаться.

С содержательной точки зрения важен следующий полученный результат. Оба измеряемых параметра - уровень рекламы и число конкурирующих книг - являются статистически значимыми. Большее влияние на уровень продаж оказывает число книг - конкурентов.

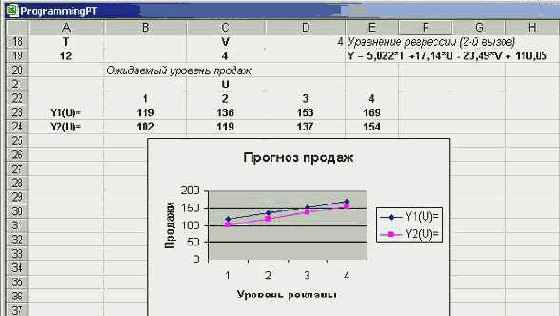
Скажу еще, что менеджер вполне обоснованно решил использовать полученные уравнения как для прогноза будущих продаж, так и для принятия таких решений, как, скажем, повышение уровня рекламы. Чтобы визуально увидеть влияние уровня рекламы на продажи, менеджер использовал полученные уравнения для построения графиков Y1(U) и Y2(U) при фиксированных значениях параметров T и V. Результаты его работы можно увидеть на следующем рисунке:

увеличить изображение
Рис. 8.27.  Прогнозирование продаж в зависимости от уровня рекламы

Полученные графики наглядно показывают, что при переходе от первого уровня рекламы к четвертому можно в полтора раза повысить продажу книг. Это предложение экономически целесообразно и менеджер представил его на рассмотрение руководителю офиса. Пусть они решают свои проблемы, а мы займемся рассмотрением других функций.

Прогнозирование нестационарных показателей

Чаще всего среднее значение спроса с течением времени меняется. Такое изменяющееся среднее принято называть трендом. Для краткосрочного прогноза часто достаточно ограничиться линейным трендом. Наиболее распространены две модели линейного тренда. При линейно-аддитивном тренде среднее изменяется на постоянную величину за время dt. В линейно-мультипликативной модели тренд меняется на постоянный процент, например, ежемесячно спрос может возрастать на 2%. Рассмотрим подробнее линейно-аддитивную модель, когда спрос меняется в соответствии с формулой:

St = a + b* t + et

Здесь et - ошибка измерения. Если параметры модели a и b постоянны, их оценки можно получить по методу наименьших квадратов. Именно такие оценки реализованы в стандартных функциях Excel, предназначенных для прогнозирования. Однако можно рассматривать методы, когда предполагается, что и сами параметры меняются во времени. Метод, предложенный Холтом, использует ту же идею взвешенного суммирования, примененную в экспоненциальном сглаживании. Вот соотношения для расчета оценки прогноза и оценки параметра b:

Pt =

*St + (1-)*(St -1 + bt -1 * dt) bt = ?*(Pt - Pt -1)/ dt + (1-?)* bt -1

Здесь dt - временной интервал между двумя последними измерениями. Прогнозируемое значение на момент времени t+t1 вычисляется по формуле:

Ft + t1 = Pt + bt * t1

Некоторым недостатком метода является необходимость эмпирического задания двух констант

и ?, задающих веса. В методе двойного сглаживания Брауна достаточно ввести одну константу. Прогнозируемое значение здесь вычисляется по формуле:

Ft + t1 = 2Pt - Qt + bt * t1

Двойное экспоненциально взвешенное среднее вычисляется из соотношения:

Qt =

Pt + (1- )Qt-1

Оценка коэффициента bt дается формулой:

bt =

/(1- )*( Pt -Qt)

Есть и другие модели краткосрочного прогнозирования тренда, например, методы Бокса-Дженкинса.

Программирование сценариев

Рассмотрим теперь объекты, обеспечивающие программное создание сценариев и дальнейшую работу с ними. Вот процедура, решающая все эти задачи:

Sub ДобавитьСценарии() 'Создание трех сценариев Dim mys As Worksheet Dim Scen As Scenario, Scens As Scenarios Set mys = ThisWorkbook.Worksheets("Лист6") With mys Set Scens = .Scenarios If .Scenarios.Count > 0 Then 'Удаление сценариев For Each Scen In Scens Scen.Delete Next Scen End If With Scens .Add Name:="Минимальный тираж", ChangingCells:=Range("J37:L37"), _ Values:=Array("5000", "0", "1,5") .Add Name:="Максимальный тираж", ChangingCells:=Range("J37:L37"), _ Values:=Array("30000", "5", "2,5") .Add Name:="Нормальный тираж", ChangingCells:=Range("J37:L37"), _ Values:=Array("10000", "2", "2") 'Запуск сценариев на выполнение For Each Scen In Scens Scen.Show Next Scen 'Построение отчета '.CreateSummary ReportType:=xlStandardSummary, _ ' ResultCells:=Range("H49,D49,B49") .CreateSummary ReportType:=xlSummaryPivotTable, _ ResultCells:=Range("H49,D49,B49")

End With End With End Sub

Рассмотрим на этом примере основные объекты и методы, связанные с применением сценариев. Рабочие листы (объекты Sheet) включают в свой состав коллекцию Scenarios. Новые элементы в эту коллекцию добавляются, как чаще всего бывает, методом Add. Параметр Name задает имя сценария, ChangingCells - изменяемые ячейки. Обычно эти ячейки располагают подряд, чтобы можно было их указать одним смежным интервалом, но делать так не обязательно - объект Range может задавать и несмежные интервалы. В параметре Comment указывается дополнительная информация, по умолчанию задается автор сценария. Эти данные выводятся в итоговом отчете. Остальные два параметра задают возможность скрытия сценария и его защиты от несанкционированного доступа, - не всегда и не всем требуется объяснять принятое решение.

Совсем просто запустить сценарий на выполнение, удалить или изменить. Для этого у объектов Scenario есть методы Show, Delete, ChangeScenario. В нашем примере методом Show все три сценария поочередно запускаются на выполнение. Чтобы процедура работала в случаях ее многократного запуска, то сценарии на рабочем листе предварительно удаляются, для чего используется метод Delete.

Для создания отчета и подведения итогов используется метод CreateSummary. У параметра ReportType, задающего тип отчета, возможны значения xlStandartSummary и xlSummaryPivotTable. С первым отчетом, принимаемым по умолчанию, Вы знакомы, во втором случае отчет определяет сводную таблицу. Параметр ResultCells позволяет задать результирующие ячейки. В отличие от работы вручную я включил в итоговый отчет сведения о трех параметрах: доходе, периоде продажи и количестве проданных книг. Объект Range здесь задает три несмежные ячейки. В процедуру включены два вызова метода CreateSummary, каждый из которых создает свой тип отчета. Один из вызовов, естественно, закомментирован. Поскольку стандартный тип отчета уже приведен, то взгляните, как выглядит сводная таблица, построенная в результате выполнения этой процедуры:

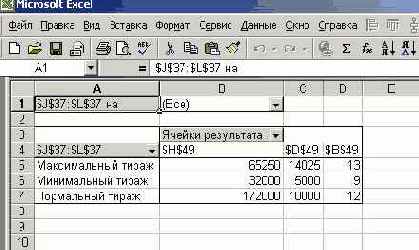
Рис. 8.36.  Сводная таблица, программно построенная по результатам выполнения сценариев

Программное формирование структуры сводной таблицы

Теперь, когда объекты PivotCache и PivotTable уже созданы, можно приступить к завершающему этапу - формированию структуры отчета сводной таблицы. Это означает, что нужно поля таблицы, содержащиеся в коллекции PivotFields распределить по измерениям. И здесь существует несколько способов выполнения этой работы. В предыдущих версиях я применял метод AddFields, который, правда, имел ряд ограничений. Теперь всю эту работу удобнее выполнять, работая непосредственно с объектами PivotField. Полного описания этих объектов давать не буду, но поясню, какими свойствами я пользовался, на примере формирования отчета сводной таблицы. Процедура, которую я сейчас приведу, полностью решает вопрос программного создания сводной таблицы, начиная от этапа связывания с источником данных, кончая этапом формирования структуры таблицы и группирования ее данных. Вот ее текст:

Public Sub MyCreatePT() 'Создание отчета сводной таблицы 'Создание кэша и отчета сводной таблицы - объектов PivotCache, PivotTable 'CreatePivotCacheAndTable 'Другой вариант создания кэша - через ADO CreatePivotCacheAndTableWithADO 'Формирование отчета сводной таблицы With ThisWorkbook.Worksheets("Лист1").PivotTables("Анализ продаж") With .PivotFields("ДатаЗаказа") .Orientation = xlRowField .Position = 1 End With With .PivotFields("Сотрудник") .Orientation = xlRowField .Position = 2 End With With .PivotFields("НазваниеКниги") .Orientation = xlColumnField .Position = 1 End With With .PivotFields("Заказчик") .Orientation = xlPageField .Position = 1 End With With .PivotFields("Стоимость") .Orientation = xlDataField .Position = 1 End With With .PivotFields("Количество") .Orientation = xlDataField .Position = 2 End With End With Range("A5").Select Selection.Group Start:=True, End:=True, By:=7, Periods:=Array(False, _ False, False, True, False, False, False) End Sub

Я приведу несколько комментариев:

На первом этапе работы создаются объекты PivotCache и PivotTable, для чего вызываются уже рассмотренные нами процедуры. Реально вызывается одна из этих процедур, вызов другой закомментирован. Какой вариант предпочесть - дело вкуса. О достоинствах этих вариантов я говорил.После создания указанных объектов формируется структура отчета сводной таблицы. Для каждого из полей сводной таблицы задается соответствующее измерение и порядок расположения. Для этого используются свойства объектов PivotField - Orientation и Position. Первое из них задает измерение, второе - порядок в измерении. Добраться до нужного поля позволяет коллекция PivotFields, где в качестве индекса используется имя поля.На заключительном шаге производится группирование данных по полю "Дата заказа". В данном случае я группирую данные по неделям. Скажу несколько слов о методе группирования данных - Group, производящем эту операцию. Он является методом класса Range и, следовательно, может вызываться объектом Selection. Здесь применяется его форма, специально созданная для группирования данных сводной таблицы. При группировании дат булев массив Periods указывает одну из 7 возможных единиц группирования (секунду, минуту, час, день, месяц, квартал, год), а параметр BY задает количество единиц в группе.

Единственное, что осталось сделать для завершения рассказа о программном создании отчета сводной таблицы, - это посмотреть на результаты работы нашей процедуры:

увеличить изображение
Рис. 8.25.  Программно построенная сводная таблица

Программное построение диаграмм с доверительными интервалами и трендами

Как это все программируется? В свое время мы рассказали о Chart-объектах, их свойствах и методах, позволяющих программно строить диаграммы. Сейчас мы на примере покажем объекты, используемые при выводе доверительных интервалов и трендов. Например, эта процедура строит доверительный интервал:

Sub ДоверительныеИнтервалы() 'Построение доверительных интервалов на диаграммме Dim myChart As Chart Dim mySeries As Series Set myChart = ThisWorkbook.Worksheets("Лист5").ChartObjects(1).Chart Set mySeries = myChart.SeriesCollection(1) mySeries.Select mySeries.ErrorBar Direction:=xlY, Include:=xlErrorBarIncludeBoth, _ Type:=xlErrorBarTypeStDev, Amount:=1 mySeries.ErrorBars.Border.Color = RGB(255, 0, 0) myChart.ChartArea.Select End Sub

Как видите, я создаю объект Chart, выделяя соответствующий ChartObject объект, встроенный в рабочий лист. Затем создаю объект класса Series, задающий ряд данных. В нашем примере диаграмма включает только один ряд, так что коллекция SeriesCollection содержит единственный элемент.

Для элемента класса Series вызывается метод ErrorBar, который и строит доверительный интервал. Значение xlErrorBarIncludeBoth параметра Include указывает на необходимость построения двухсторонних границ интервала погрешностей, а тип ошибок задается параметром Type, параметр Amount задает количество единиц в интервале погрешностей. Чем шире интервал, тем выше вероятность попадания истинного значения в указанный интервал. Доверительный интервал выделяется заданным цветом.

Следующая процедура демонстрирует построение тренда:

Sub ЛинейныйТренд() 'Построение трендов на диаграммме Dim myChart As Chart Dim mySeries As Series Set myChart = ThisWorkbook.Worksheets("Лист5").ChartObjects(1).Chart Set mySeries = myChart.SeriesCollection(1) mySeries.Select mySeries.Trendlines.Add(Type:=xlLinear, Forward:=3, _ Backward:=0, DisplayEquation:=True, DisplayRSquared:=True).Select mySeries.Trendlines.Add(Type:=xlPolynomial, Order:=3, Forward:=3, _ Backward:=0, DisplayEquation:=True, DisplayRSquared:=True).Select

myChart.ChartArea.Select End Sub

На одной диаграмме можно построить несколько трендов различного типа. Поэтому в состав объекта Series входит коллекция TrendLines, элементы которой создаются при вызове метода Add. Параметр Type задает один из 6 возможных типов тренда, параметры Forward и Backward задают интервалы прогнозируемых значений. Соответственно прогноз делается вперед и/или назад. Булев параметр DisplayEquation включает вывод уравнения регрессии в окне диаграммы.

Процедура строит на одной диаграмме два тренда - линейный и полиномиальный. Заметьте, для полиномиального тренда задается дополнительный параметр Orde, определяющий степень аппроксимирующего полинома.

Вот как выглядит лист с диаграммой, после того, как отработали рассмотренные нами процедуры:


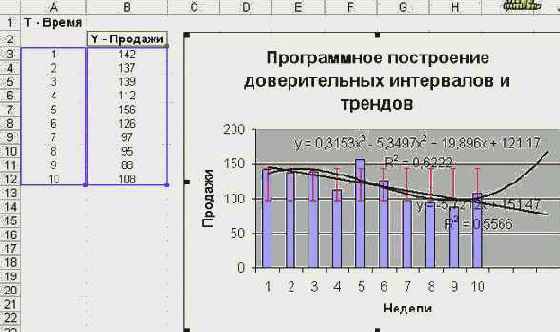
увеличить изображение
Рис. 8.29.  Программно построенные доверительные интервалы и тренды

Но вернемся к менеджеру "РР". Визуальный анализ данных показал, что, вряд ли, результаты продаж хорошо согласуются с моделью линейного или полиномиального тренда. Менеджер просмотрел все виды трендов: ни один из них не учитывал в полной мере характер поведения данных. Один из них при прогнозе дает слишком пессимистическую оценку, другой - излишне оптимистическую. Полином третьей степени неплохо описывает поведение данных, но только на интервале наблюдения. Использовать его для целей прогноза, очевидно, невозможно. Увы, такая ситуация типична. Модель, особенно полиномиальная, может хорошо описывать наблюдаемые значения, но не годиться для прогноза.

Дело здесь не в том, что используемые для прогноза функции плохи, дело в самой модели. Заметьте, на построенной диаграмме продажи строятся как функция от времени и никак не учитываются другие факторы, которые влияют на продажи. Я напомню, что менеджер при построении уравнения регрессии понимал это и строил это уравнение, как функцию, зависящую от трех факторов - времени, уровня рекламы, числа конкурирующих книг. Он понимал, что модель, используемая для прогноза, должна учитывать все факторы, оказывающие существенное влияние на прогнозируемую величину.

Приведенный здесь визуальный анализ продаж, как функции от времени, способен скорее убедить менеджера в том, что на уровень продаж влияет не только время, но и другие факторы. Оставим менеджера в размышлениях, а сами пока познакомимся еще с некоторыми стандартными средствами Office 2000, связанными с анализом "Что, если ...?".



myChart.ChartArea.Select End Sub

На одной диаграмме можно построить несколько трендов различного типа. Поэтому в состав объекта Series входит коллекция TrendLines, элементы которой создаются при вызове метода Add. Параметр Type задает один из 6 возможных типов тренда, параметры Forward и Backward задают интервалы прогнозируемых значений. Соответственно прогноз делается вперед и/или назад. Булев параметр DisplayEquation включает вывод уравнения регрессии в окне диаграммы.

Процедура строит на одной диаграмме два тренда - линейный и полиномиальный. Заметьте, для полиномиального тренда задается дополнительный параметр Orde, определяющий степень аппроксимирующего полинома.

Вот как выглядит лист с диаграммой, после того, как отработали рассмотренные нами процедуры:


увеличить изображение
Рис. 8.29.  Программно построенные доверительные интервалы и тренды

Но вернемся к менеджеру "РР". Визуальный анализ данных показал, что, вряд ли, результаты продаж хорошо согласуются с моделью линейного или полиномиального тренда. Менеджер просмотрел все виды трендов: ни один из них не учитывал в полной мере характер поведения данных. Один из них при прогнозе дает слишком пессимистическую оценку, другой - излишне оптимистическую. Полином третьей степени неплохо описывает поведение данных, но только на интервале наблюдения. Использовать его для целей прогноза, очевидно, невозможно. Увы, такая ситуация типична. Модель, особенно полиномиальная, может хорошо описывать наблюдаемые значения, но не годиться для прогноза.

Дело здесь не в том, что используемые для прогноза функции плохи, дело в самой модели. Заметьте, на построенной диаграмме продажи строятся как функция от времени и никак не учитываются другие факторы, которые влияют на продажи. Я напомню, что менеджер при построении уравнения регрессии понимал это и строил это уравнение, как функцию, зависящую от трех факторов - времени, уровня рекламы, числа конкурирующих книг. Он понимал, что модель, используемая для прогноза, должна учитывать все факторы, оказывающие существенное влияние на прогнозируемую величину.

Приведенный здесь визуальный анализ продаж, как функции от времени, способен скорее убедить менеджера в том, что на уровень продаж влияет не только время, но и другие факторы. Оставим менеджера в размышлениях, а сами пока познакомимся еще с некоторыми стандартными средствами Office 2000, связанными с анализом "Что, если ...?".

Программное построение сводных таблиц

Создать серьезную систему анализа деятельности офиса без программирования невозможно. Наряду с построением сводной таблицы вручную программист должен уметь написать и соответствующую программу. Допустим, Вы разрабатываете в Вашем приложении подсистему "Помощник Аналитика". Конечно, здесь не обойтись без сводных таблиц, и строиться они должны щелчком одной кнопки с дальнейшим диалогом, настроенным на конкретную проблему.

Рассмотрим объектную модель, используемую при программной работе со сводными таблицами, - основные классы, их свойства и методы. Для краткости я буду называть соответствующие объекты "Pivot-объектами". Нужно заметить, что модель Pivot-объектов достаточно сложная, она включает несколько классов, многие из которых имеют достаточно большой набор свойств и методов. Замечу, что эта объектная модель в Office 2000 претерпела существенные изменения в сравнении с предыдущей версией. Существенное влияние на нее оказал новый подход к доступу данных, основанный на OLE DB и ADO. С этой точки зрения, знакомство с ADO поможет нам и при изучении модели Pivot-объектов.

Замечу, документация по этим объектам, как мне кажется, оставляет желать лучшего. Она не полна, не всегда точна. Замечу еще, что и использование такого средства, как Macrorecorder, не дает правильного представления о том, как использовать новые возможности Pivot-объектов, поскольку Macrorecorder работает, основываясь на старой модели.

Два основных класса объектов - PivotCache и PivotTable и две коллекции этих объектов - PivotCaches и PivotTables играют центральную роль в программном создании сводных таблиц. Кроме них существует еще несколько классов, так или иначе связанных со сводными таблицами:

PivotField и коллекция PivotFields - определяют поля сводной таблицы,PivotItem и коллекция PivotItems - определяют данные, хранимые в полях сводной таблицы,PivotLayout и коллекция PivotLayouts - определяют расположение полей сводной таблицы,

Поговорим об основных объектах. Прежде всего, разберемся с тем, почему понадобились два объекта (два класса), чтобы описать одну сущность - сводную таблицу. Объект PivotCache задает кэш-память, сводную таблицу, хранимую в оперативной памяти, ее данные. Работа с этим объектом, помимо всего прочего, позволяет оптимизировать память, отводимую сводной таблице. Объект PivotTable задает представление сводной таблицы на рабочем листе, задает отчет. До сих пор я не использовал термин "отчет" сводной таблицы, хотя он широко используется, в том числе и в документации. Теперь пришла пора и для этого термина. Действительно, объект PivotTable вполне соответствует понятию отчета, задаваемого сводной таблицей. Таким образом, два объекта PivotCache и PivotTable задают внутренне и внешнее представление сводной таблицы. В основе объекта PivotTable лежит объект PivotCache, являясь источником данных для объекта PivotTable.

Правильная технология работы при программном создании сводной таблицы состоит в том, чтобы вначале создать объект PivotCache, а затем на его основе создать объект PivotTable. Заметьте, если объект PivotCache создан, но не создан объект PivotTable, ссылающийся на этот кэш памяти, то при закрытии документа память освобождается и объект PivotCache автоматически удаляется перед сохранением рабочей книги.

Есть некоторая разница и в коллекциях этих объектов. Коллекция PivotCaches связана с самой книгой - объектом Workbook, в то время как коллекция PivotTables связывается с рабочим листом - объектом WorkSheet. А теперь перейдем к деталям и рассмотрим подробнее основные свойства и методы этих классов объектов.

Программное построение таблиц подстановки

Ну и несколько слов о том, как построить таблицу подстановки программно. Если подготовительная работа уже выполнена, - созданы заголовки таблицы и записана формула, вычисляющая функцию от двух параметров, то дальнейшее построение таблицы подстановки выполняется одним оператором. Достаточно выделить соответствующую прямоугольную область под таблицу и вызвать метод Table объекта Selection или Range. Метод имеет два параметра, задающих ячейки ввода.

Вот процедура, которая на другом месте строит таблицу подстановки, аналогичную той, которая показана на предыдущем рисунке 8.30:

Public Sub Buildtable() 'Программное построение таблицы подстановки Dim myr As Range Set myr = Range("A1:H7") myr.Clear 'Построение заголовков таблицы подстановки Range("E1") = "Уровень рекламы" Range("A5") = "Число конкурентов" Range("C2") = 0: Range("D2") = 1 Range("C2: D2").AutoFill Destination:=Range("C2:H2"), Type:=xlFillDefault Range("B3") = 0: Range("B4") = 1 Range("B3: B4").AutoFill Destination:=Range("B3:B7"), Type:=xlFillDefault Range("B2").Formula = "= 8.318*$B$13 + 16.66*$A$1-26.58*$A$2 +109.06" 'Формирование таблицы Set myr = Range("B2:H7") myr.Table RowInput:=Range("A1"), ColumnInput:=Range("A2")

End Sub

Сценарии

Таблицы подстановки применимы, когда результат, точнее функция, его вычисляющая, зависит максимум от двух параметров. При анализе более сложных моделей, когда результат зависит от большего количества факторов, следует использовать другое средство - сценарии. Заметьте, даже в рассматриваемой нами достаточно простой ситуации уровень продаж зависит от трех параметров - времени, уровня рекламы и числа конкурентов.

Итак, пусть результирующая функция F(a1,a2, …an) зависит от n параметров. Сценарием будем называть набор значений этих параметров. Добавить новый сценарий в коллекцию означает ввести новый набор значений параметров и связать с ним имя сценария. Ячейки, хранящие параметры, на которые ссылается функция F, называются изменяемыми. При выборе сценария в них будут посланы значения, заданные этим сценарием. После чего будет вычислено соответствующее значение результирующей функции. Результаты вычислений по всем сценариям можно объединить в одной сводной таблице.

Такова основная идея сценариев. Их можно рассматривать, как некоторое обобщение таблиц подстановки. Как обычно, создать и анализировать сценарии можно вручную или программно. Мы рассмотрим оба способа. Но вначале обсудим задачу, требующую введения сценариев.

Сезонный спрос

Сезонные колебания действуют независимо от других факторов и накладываются на ту или иную модель спроса. Проще всего учесть сезонный фактор, используя коэффициенты сезонности. Так, если, как обычно, принять сезонный цикл за год, можно иметь 52 недельных или 12 месячных коэффициентов сезонного спроса. Коэффициент сезонности представляет собой отношение среднего спроса за текущий период ( месяц) к среднему значению за весь период цикла (год). Чтобы оценить значения коэффициентов сезонности, требуются данные за несколько лет. Достоверность результатов обычно можно повысить за счет того, что сезонные циклы одинаковы для разных товаров.

Если сезонные коэффициенты рассчитаны, то учет сезонности не вызывает трудностей для любой из моделей тренда. Вначале необходимо текущие значения очистить от влияния сезонности делением на соответствующий коэффициент. Затем применить обычный алгоритм прогноза и полученную прогнозную оценку умножить на коэффициент сезонности, соответствующий моменту прогноза.

Среднесрочный прогноз и методы регрессионного анализа

Для среднесрочного прогноза обычно применяются методы регрессионного анализа. Хотя ничто не мешает применять их и для краткосрочного прогноза. Они основаны на получении оценок по методу наименьших квадратов. Эти методы и реализованы в стандартных функциях Excel, так что рассмотрим их подробнее. Начнем с наиболее простой модели линейного тренда. В основе модели лежит уже упоминавшееся соотношение:

Yt = a + b* t + Et

Это соотношение можно интерпретировать следующим образом. В каждый момент времени t измеренное значение спроса Yt является суммой неизвестной помехи Et и линейной функции времени с неизвестными (ненаблюдаемыми) параметрами a и b. Из-за помех решения, принимаемые на основе измерений, носят вероятностный характер. Найти точные значения параметров a и b в этих условиях невозможно, но, зная выборку Yt, можно вычислить оценки параметров. В статистике оценкой называют любую функцию от измерений. Оценки параметров a и b можно получить по методу наименьших квадратов из условия минимизации квадратичного функционала:

F(a, b) =

(Yt - (a +b*t))2

При этом, когда мы имеем дело с линейной моделью, минимум этого функционала находится аналитически, и в случае двух параметров можно явно выписать конечные соотношения для оценок параметров a и b. В этом одно из преимуществ метода наименьших квадратов. Прямая Yt = в + ^b* t , где a и ^b - оценки параметров, называется линией регрессии и используется для прогнозирования значений Y в произвольные моменты времени t. Конечно, чем дальше отстоит значение t от интервала наблюдений, тем вероятнее, что ошибка прогноза будет увеличиваться.

Метод наименьших квадратов хорош и с точки зрения статистики. Если предположить, что неизвестные нам помехи распределены по нормальному закону с нулевым математическим ожиданием и, в общем случае, с заданной корреляционной матрицей, то полученные оценки обладают важными свойствами несмещенности, состоятельности и эффективности. Мы не будем давать строгого определения всех этих терминов. Скажем лишь, что в классе несмещенных оценок наши оценки обладают минимальной дисперсией, т. е. минимальным разбросом относительно истинного значения параметров. Чем больше измерений, тем точнее оценки, так как уменьшается интервал, накрывающий истинное значение параметра с заданной вероятностью. Как ни странно, но практика показала, что предположения о характере помех зачастую оправдываются. В теории вероятностей этому факту есть хорошее объяснение. Недаром открытый Гауссом закон распределения называется "нормальным". Все в нашей жизни распределено по гауссиане.

Обобщим теперь постановку задачи на произвольное количество параметров, полагая теперь, что спрос может быть описан уже не линейной, а полиномиальной функцией времени, например:

Yt = a0 + a1 t + a2t2 + … + amtm + Et

Это полиномиальное относительно времени соотношение остается линейным по отношению к неизвестным параметрам. Для простоты перейдем к матричной форме записи соотношений:

Y = X*a + E

Здесь Y - вектор измерений, a - вектор параметров, E - вектор ошибок, X - прямоугольная матрица, элементы которой зависят от t и не зависят от параметров a. Для полиномиальной зависимости нетрудно выписать явный вид ее элементов:

X = || ti j.|| i= 1…n; j = 0..m;

Число строк этой матрицы определяется моментами времени t1, t2, … tn, в которые производились измерения, а количество столбцов определяется степенью полинома. Квадратичный функционал F(a) в матричной форме имеет вид:

F(a) = (Y - X*a)T R-1 (Y - X*a)

Продолжая обобщать постановку задачи, мы ввели корреляционную матрицу R ошибок измерений. В частном случае, когда отсутствует корреляция ошибок измерений и дисперсия их единична, матрица R превращается в единичную матрицу. Другой важный частный случай - диагональный, когда корреляция отсутствует, но дисперсия ошибки меняется от измерения к измерению. Величину, обратную к дисперсии -1/?2 , можно рассматривать как вес измерения. Так что введение этой матрицы позволяет приписать разный вес измерениям, придавая, например, больший вес последним измерениям.

Все эти обобщения не нарушают возможности получения аналитического решения. Вектор оценок a, минимизирующий квадратичный функционал F(a), определяется по формуле:

a = I-1 XT R-1 Y

Здесь I - информационная матрица Фишера, вычисляемая из соотношения:

I = XT R-1 X

Наряду с вектором оценок нетрудно получить и его статистические характеристики. Поскольку оценки являются несмещенными, для полного знания распределения вектора оценок достаточно знать его корреляционную матрицу. В данном случае она является обратной к матрице Фишера.

Ra = I-1

Даже если исходные измерения независимы, между оценками параметров может возникать корреляция. Правда, на практике чаще всего используют только значения их дисперсий.

До сих пор мы рассматривали временные ряды, и в наших измерениях присутствовал только один наблюдаемый параметр - время. В регрессионном анализе обычной ситуацией является проведение измерений, когда в каждой точке фиксируется несколько наблюдаемых параметров, влияющих на измеряемое значение. Применительно к задаче спроса такими параметрами могут быть, например, уровень текущей рекламы, количество конкурирующих товаров, погодные условия. Так что линейная относительно неизвестных параметров модель спроса в общем случае может быть такой:

Yi = a0 + a1 x1i + a2x2i+ … + amxmi + Ei



В матричной форме записи все соотношения остаются справедливыми, изменяются лишь соотношения для расчета элементов матрицы X. В заключение отметим, что при долговременном прогнозировании предположение о линейности тренда вряд ли справедливо, кривая спроса имеет более сложную форму и не описывается линейной функцией относительно параметров. В этом случае определить аналитически точку минимума квадратичного функционала F(a), обычно уже невозможно. Правда, есть одно важное исключение. Пусть:

Yi = F(a0 + a1 x1i + a2x2i+ … + amxmI)+ Ei

и функция G является функцией, обратной к F. Тогда линейная модель по-прежнему имеет место, но уже для преобразованных значений измерений:

G(YI )= (a0 + a1 x1i + a2x2i+ … + amxmI)+ Ei

С точки зрения статистики это преобразование измерений нарушает предположение о нормальном характере поведения измерений. Если закон распределения Yi был нормальным, то закон распределения G(Yi) таковым уже не будет. Поэтому найденные оценки лишаются теоретически обоснованного хорошего качества их поведения. На практике же такие процедуры применяют часто.

Но вовсе не обязательно приводить нашу модель к линейной относительно параметров. Она спокойно может оставаться нелинейной, так как существуют хорошо разработанные численные методы. Более того, можно использовать для минимизации функционала средство самого Excel - Решатель. Думается, найти минимум функционала не столь сложно - сложнее построить адекватную реальной ситуации модель спроса. Здесь надо выяснить, какие параметры, влияющие на спрос, поддаются прямому наблюдению, а какие требуется оценить по результатам наблюдений. Не менее сложно подобрать аналитическое описание кривой спроса с точностью до неизвестных параметров. Таким образом, экономисту, математику и программисту есть где поработать, создавая эффективную систему прогноза. Средства Office 2000, прежде всего Excel, облегчают решение этой задачи, а нередко позволяют получить ее решение на основе встроенных стандартных функций.

Структура сводной таблицы

Сводную таблицу можно рассматривать как таблицу с тремя измерениями, в каждой точке которой заданы данные. Четыре оси сводной таблицы носят названия:

Оси Строк;Оси Столбцов;Оси Страниц, называемой также осью Фильтров;Оси Данных.

Если бы на каждой оси располагались значения одного типа, то эта модель была бы совершенно простой и понятной. Можно было бы рассматривать сводную таблицу, как функцию трех переменных - F(x,y,z), заданную таблицей. Вся сложность сводной таблицы состоит в том, что на каждой оси может располагаться несколько полей, это же верно и относительно данных, - полей данных может быть также несколько. Поэтому, каждая из координат сводной таблицы, также как и значение функции F, представляет собой агрегат довольно сложной структуры. Поля, располагаемые на той или иной оси, получают тип этой оси - поля строк, поля столбцов, поля фильтра, поля данных.

Важным свойством сводной таблицы является то, что ее структуру можно легко менять в процессе работы с этой таблицей. Поля, располагаемые на оси, жестко не закрепляются, и, при желании, можно в ходе работы изменять структуру таблицы, меняя местами, например, поля строк и столбцов.

Заметьте, что при таком определении сводной таблицы, ее трехмерность носит довольно условный характер, реально измерений значительно больше, и сводная таблица представляет собой гиперкуб - многомерный куб данных.

Чтобы пояснить ситуацию со структурой сводной таблицы, приведу простой пример, когда на каждой оси располагается ровно одно поле. Рассмотрим организацию, занимающуюся продажами. При построении сводной таблицы на оси страниц (фильтров) расположим поле "Отделы", на оси строк - поле "Сотрудники", на оси столбцов - поле "Месяцы". Единственное поле данных "Продажи" будет задавать объем продаж. Тогда, если выбрать соответствующий отдел, или, другими словами, включить фильтр по отделам, строки таблицы будут задавать имена сотрудников выбранного отдела, столбцы будут задавать месяцы, а значения на пересечении строки и столбца будут определять объем продаж, совершенных данным сотрудником данного отдела в данном месяце. Для этой таблицы достаточно естественно ввести группирование данных, как по строкам, так и по столбцам. Например, сотрудников отделов можно сгруппировать по лабораториям, а месяцы - по кварталам. Тогда легко получать представление данных с разной степенью детал

изации, например, сравнить данные о продажах отдельных лабораторий за определенный квартал. Реальные сводные таблицы бывают значительно более сложными, хотя бы по той причине, что на каждой оси располагаются несколько различных полей, а уровней группирования данных может быть более двух.

Еще одно немаловажное достоинство сводных таблиц состоит в том, что они могут сопровождаться сводными диаграммами, которые визуально отображают данные таблицы, мгновенно изменяясь при очередных манипуляциях над таблицей.

Подводя первые итоги, отметим, что сводные таблицы имеют сложную структуру. Данные в этих таблицах легко группировать и разгруппировывать. Поля таблицы можно скрывать и делать видимыми. Структуру таблицы легко видоизменять. Сводная таблица позволяет консолидировать однотипные данные, хранящиеся в разных источниках. К тому же в таблице выполняется автоматическое подведение итогов и возможно применение других обобщающих функций, например, расчет средних значений.

Чаще всего в роли источника данных для построения сводной таблицы выступают базы данных. Это могут быть табличные (реляционные) базы данных, например, Access или Microsoft SQL Server, В последнее время в качестве источников данных стали широко применяться кубы OLAP. Между кубами OLAP и сводными таблицами много общего. Эти объекты, в какой-то мере, близнецы - братья. Кубы OLAP служат для хранения многомерных данных, а сводные таблицы для проведения анализа этих данных.

Сводные диаграммы

При работе со сводными таблицами визуализация данных способствует правильному их восприятию. Поэтому чаще всего наряду со сводной таблицей строится и соответствующая ей сводная диаграмма. Задать построение диаграммы можно еще на первом шаге работы Мастера сводных таблиц, что показано на рис.8.1. Однако сделать это не поздно и потом, когда таблица уже построена. Среди кнопок инструментальной панели есть и кнопка, нажатие которой приводит к построению сводной диаграммы на отдельном листе. Взгляните, как выглядит лист со сводной диаграммой:

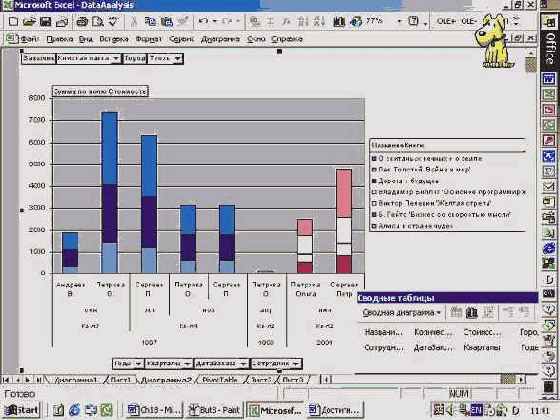
увеличить изображение
Рис. 8.18.  Лист со сводной диаграммой

Заметьте, на лист диаграмм вынесены и поля таблицы, что позволяет задавать фильтры, мгновенно изменяя диаграмму. При работе с листом диаграммы доступны и кнопки инструментальной панели.

Еще раз отмечу, диаграмма и сводная таблица жестко связаны, - любые изменения в диаграмме и сводной таблице взаимосвязаны.

Свойства и методы объекта PivotCache

У объекта PivotCache 23 свойства. Большинство из них я рассмотрю:

Connection - позволяет задать соединение с источником данных. Возвращает или устанавливает строку, имеющую разный синтаксис в зависимости от типа источника данных. Строка может задавать: OLE DB установки для связи Excel с OLE DB источниками данных,ODBC установки для связи Excel с ODBC источниками данных,URL, когда Excel связывается с данными Web-страниц,Полный путь, задающий текстовый файл или файл, задающий Web-запрос или базу данных.

Строка начинается специальным ключевым словом, указывающим тип источника данных. В зависимости от варианта префикс, начинающий строку соединения, имеет вид - OLEDB; ODBC; URL; TEXT. Префикс заканчивается символом ";" (точка с запятой). В остальном, строка удовлетворяет требованиям, предъявляемым к строке соединения при работе с ADO. Вот пример задания свойства Connection для соединения с базой данных Access с использованием провайдера Microsoft Jet:

ActiveWorkbook.PivotCaches.Add(SourceType:=xlExternal).Connection = _ "OLEDB; Provider=Microsoft.jet.oledb.4.0;" & _ "Data Source=c:\!O2000\DSCD\Ch18\dbPP2000.mdb"

Установка значения для свойства Connection не означает непосредственного соединения с источником данных. Необходимо вызывать метод Refresh, чтобы такая связь была в действительности установлена.LocalConnection, UseLocalConnection - эти два свойства используются при работе с сохраненными в отдельном файле OLAP кубами. Когда в качестве источника данных используется OLAP куб, то вместо задания свойства Connection следует использовать свойство LocalConnection, предварительно установив значение True для свойства UseLocalConnection.CommandType, CommandText - два хорошо знакомых по ADO свойства. Первое из них определяет тип команды, а второе значение команды, выполняющей запрос к источнику данных. Первое свойство может иметь четыре значения, заданное константами: xlCmdCube, xlCmdDefault, xlCmdSQL, xlCmdTable. В зависимости от установленного значения свойство CommandText задает: Имя куба для OLAP кубов,Текст команды, учитывающий специфику и требования провайдера,Текст SQL-запроса,Имя таблицы.MemoryUsed As Long - свойство имеет статус "только для чтения", возвращает количество байтов памяти занятой в текущий момент под кэш. Если объект PivotTable не присоединен к объекту PivotCache, то возвращается значение 0.OptimizeCache - булево свойство, при установке значения True, кэш будет оптимизироваться при его конструировании. Для OLE DB источников данных свойство имеет статус "только для чтения" и имеет значение по умолчанию - False.QueryType - свойство имеет статус "только для чтения", возвращает константу типа xlQueryType, которая определяет тип запроса, используемого Excel для заполнения кэша.Recordset - очень важное и полезное свойство при программной работе со сводными таблицами. Оно позволяет вернуть или установить хорошо знакомый объект Recordset, задающий набор записей, используемый при построении кэша. Тем самым появляется возможность программного создания и наполнения данными объекта PivotCache. Связь с источником данных можно организовать средствами ADO и получить объект Recordset. После чего остается только установить свойство объекта PivotCache. Зачастую, это более эффективный способ работы с источником данных. Пример такого способа работы будет приведен.RecordCount - как обычно, задает число записей в наборе Recordset.RefreshDate, RefreshName, RefreshOnFileOpen, RefreshPeriod - свойства, задающие различную информацию, связанную с обновлением данных.

Рассмотрим теперь методы объекта PivotCache. Их немного - всего три:
Function CreatePivotTable(TableDestination, [TableName], [ReadData]) As PivotTable. Этот метод (функция) создает объект PivotTable, основанный на данном кэше - объекте PivotCache. Это основной способ создания и появления объектов PivotTable. Аргумент TableDestination представляет объект Range, задающий область построения сводной таблицы. Аргумент задает ячейку в левом верхнем углу этой области. Напомню, что объект PivotTable связан с определенным листом рабочей книги, поэтому аргумент должен определять и нужный рабочий лист, в противном случае будет выбран активный лист рабочей книги.Аргумент TableName задает имя сводной таблицы - имя объекта PivotTable, которым можно пользоваться при работе с коллекцией PivotTables.Булев аргумент ReadData позволяет установить способ чтения записей в кэш. Он имеет значение True, если в кэш читаются все записи.Sub Refresh(). Обновляет кэш текущим состоянием источника данных.Sub ResetTimer(). Восстанавливает значение таймера. Это может быть важно, когда используется свойство RefreshPeriod, задающее период времени между последующими обновлениями источника данных.
На этом я закончу рассмотрение свойств и методов объекта PivotCache. Примеры создания этого объекта приведу чуть позже, после рассмотрения объекта PivotTable, поскольку создавать эти объекты, тесно связанные между собой, следует в одной процедуре.

Свойства и методы объекта PivotTable

Объект PivotTable, задающий отчет сводной таблицы - его внешнее представление устроен, естественно, более сложно. У него значительно больше свойств, чем у объекта PivotCache, - их 54, да и методов в четыре раза больше. Замечу, что для программного создания сводной таблицы достаточно использовать лишь малую часть из этого набора. Большая часть этих свойств и методов необходима, если Вы хотите программно поддерживать работу пользователя со сводной таблицей.

Давайте рассмотрим основные свойства этого объекта:

ColumnFields([Index]) As Object, DataFields([Index]) As Object, PageFields([Index]) As Object, RowFields([Index]) As Object. Все эти свойства имеют статус "только для чтения" и возвращают коллекцию или отдельный элемент коллекции, если указан индекс. Возвращаемые объекты задают поля сводной таблицы по соответствующему измерению - поля столбцов, данных, страниц или строк. Вне зависимости от измерения все возвращаемые объекты принадлежат единому классу PivotField или PivotFields для коллекций.ColumnRange, DataLabelRange, DataBodyRange, PageRange, RowRange - возвращают объект Range, задающий соответствующую область. Вот простенькая процедура, поочередно выделяющая указанные области сводной таблицы:

Public Sub SelectRange() ThisWorkbook.Worksheets("Лист1").Activate Range("A3").Select ActiveCell.PivotTable.ColumnRange.Select ActiveCell.PivotTable.DataLabelRange.Select ActiveCell.PivotTable.DataBodyRange.Select ActiveCell.PivotTable.PageRange.Select ActiveCell.PivotTable.RowRange.Select End SubColumnGrand, RowGrand - булевы свойства, имеющие значение True, если сводная таблица подводит итоги по столбцам и строкам.CubeFields - для сводных таблиц, основанных на OLAP кубе, возвращает одноименную коллекцию, задающую поля куба. Каждый объект этой коллекции содержит свойства поля.HiddenFields([Index]) As Object, VisibleFields([Index]) As Object - коллекции спрятанных и видимых полей. Для сводных таблиц, основанных на OLAP кубах спрятанных полей нет - все поля являются видимыми.ErrorString As String, DisplayErrorString As Boolean. Первое из свойств позволяет задать строку, представляющую сообщение об ошибке, второе - позволяет включить или отключить появление этой строки в вычисляемых полях, где возникает ошибка.PivotFormulas As PivotFormulas - возвращает одноименную коллекцию объектов. Каждый элемент этой коллекции является объектом класса PivotFormula и представляет формулу, используемую в вычисляемых полях.

На этом я закончу рассмотрение свойств и перейду к рассмотрению методов:
Function AddFields([RowFields], [ColumnFields], [PageFields], [AddToTable]). Позволяет добавить поля к соответствующему измерению. Последний булев параметр позволяет указать, будут ли поля добавляться или заменять существующий набор полей. В предыдущей версииFunction CalculatedFields() As CalculatedFields. Возвращает одноименную коллекцию вычисляемых полей.Sub Format(Format As xlPivotFormatType). Производит форматирование сводной таблицы. Аргумент Format задает один из возможных типов форматирования.Function GetData(Name As String) As Double. Позволяет получить данные из отдельной ячейки сводной таблицы. Аргумент Name задает поля таблицы, однозначно определяющие ячейку. Он имеет достаточно сложный синтаксис, на деталях которого останавливаться не буду.Function PivotCache() As PivotCache - возвращает объект PivotCache, связанный с отчетом.Function PivotFields([Index]) As Object - возвращает одноименную коллекцию, а при указании индекса элемент этой коллекции, задающий поле сводной таблицы. В качестве индекса можно использовать имя поля. Возвращаемые объекты принадлежат классу PivotField. Позже в примере я продемонстрирую работу с этими объектами при программном формировании структуры сводной таблицы.Sub PivotTableWizard([SourceType], [SourceData], [TableDestination], [TableName], [RowGrand], [ColumnGrand], [SaveData], [HasAutoFormat], [AutoPage], [Reserved], [BackgroundQuery], [OptimizeCache], [PageFieldOrder], [PageFieldWrapCount], [ReadData], [Connection]). Этим методом, но не в виде процедуры, а в виде функции обладает и объект Worksheet. Вызванный этим объектом метод позволяет создать объект PivotTable. В предыдущих версиях Office этот способ был основным для создания подобных объектов. Теперь надобность в нем практически отпала. Метод моделирует работу Мастера сводных таблиц и имеет многочисленные аргументы, позволяющие определить сводную таблицу. Поскольку, как я сказал, теперь не следует пользоваться этим методом, то я не буду останавливаться на деталях его описания.Function RefreshTable() As Boolean - обновляет данные сводной таблицы и возвращает значение True, если обновление прошло удачно.Function ShowPages([PageField]) - создает новый отчет для каждого элемента в поле страниц. Каждый отчет создается на отдельной странице.

Таблицы подстановок, Сценарии и Поиск решения

Таблица подстановок - одно из средств анализа данных. Вот первая задача, которая приводит к построению таблицы подстановок. Рассмотрим набор функций, зависящих от одного и того же параметра: F1(a), F2(a), …Fm(a). Пусть каждая из этих функций задается формулой Excel. Пусть также требуется проанализировать зависимость этих функций от значений параметра a. Обычно нас интересуют результаты для конечного набора значений параметра - a1, a2, …an. В этом случае все, что нужно для анализа, - это построить прямоугольную таблицу размерности n*m, элементами которой будут значения Fj(ai). Excel позволяет без особого труда построить такую таблицу. Таблицы подстановок упрощают решение этой задачи.

Чтобы вручную построить такую таблицу, надо записать в столбец значения ai, в строку, расположенную на одну ячейку выше и правее, записать формулы Fj(Ain). Все формулы должны ссылаться на одну и ту же ячейку Ain - ячейку ввода. Можно, конечно, значения параметра записать в строку, а формулы в столбец. Основное требование к расположению формул и значений параметра состоит в том, чтобы они определяли прямоугольную область таблицы и воспринимались как заголовки ее строк и столбцов. Проделав эту подготовительную работу, достаточно выделить прямоугольную область, занятую таблицей, включая заголовки, и выбрать в меню "Данные" пункт "Таблица подстановок". В появившемся окне нужно задать ссылку на ячейку ввода. Заметьте, если значения параметра располагаются в столбец, то ссылку на ячейку ввода нужно задавать в окне строк, а не в окне столбцов. По щелчку кнопки OK таблица значений Fj(ai) будет автоматически построена.

Другая задача, приводящая к таблице подстановок, состоит в том, что рассматривается только одна функция F(a,b), но теперь зависящая от двух параметров. Элементами таблицы являются значения этой функции F(ai, bj). В роли заголовков строк и столбцов выступают значения ai и bj. Для записи формулы осталось одно свободное место - ячейка в левом верхнем углу таблицы. Формула, записанная в нее, ссылается теперь на две ячейки ввода - ячейку ввода строки и ячейку ввода столбца. Этим нюансом в расположении заголовков отличаются подготовительные действия по созданию таблицы подстановок в первом и во втором случае. Остальные действия аналогичны. И здесь нужно быть аккуратным в выборе окон при задании ссылок. Мне, например, всегда хочется задавать ссылки в другом порядке.

Конечно, таблицы подстановки - не столь уж мощное средство анализа данных. Собственно говоря, никакого анализа данных они не выполняют. Это лишь часто используемое средство, облегчающее построение таблицы данных для ее визуального анализа. Таблицу анализирует сам пользователь, исходя из содержательных соображений. Обычно, только он может понять, какие значения параметров a и b наиболее подходят для его целей. Хотя, конечно, может существовать и формальный алгоритм выбора из таблицы наилучшего значения.

А теперь покажем, как менеджер офиса использует таблицу подстановки в своем анализе. Ранее он построил уравнение регрессии, в котором продажи зависят от уровня рекламы и количества конкурирующих книг. Менеджер уже использовал его для прогноза состояния продажи книги и даже построил соответствующие графики, демонстрирующие прогнозируемую зависимость продаж от уровня рекламы. Однако графики были построены для фиксированного числа конкурирующих книг. Менеджер не определил еще окончательно, каков будет уровень рекламы в точке прогноза, и тем более он не знает точного значения количества конкурентов. Поэтому он решает построить таблицу подстановки, чтобы оценить все реально возможные варианты. Вот что у него получилось:

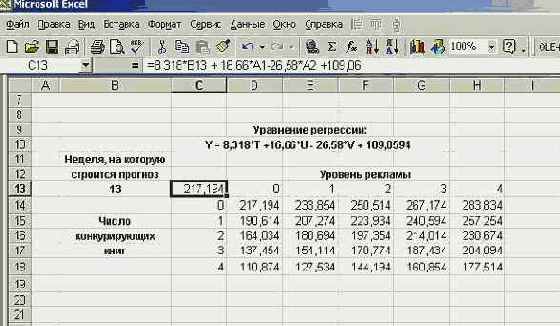
увеличить изображение
Рис. 8.30.  Таблица подстановки, используемая в анализе "Что, если ...?"

Эта таблица позволяет ему получить ответы на вопросы: каков прогноз на продажу книг на следующий месяц и что будет, если появится новый конкурент, и что будет, если повысить уровень рекламы?

Встроенные функции Excel и прогнозирование

Для решения задач прогнозирования в Excel встроены несколько функций. По существу все они сводятся к нахождению оценок по методу наименьших квадратов в задаче линейной регрессии. Наряду с оценками вычисляются и их статистические характеристики, что позволяет строить доверительные интервалы и делать выводы, имеющие вероятностный характер.

Задача менеджера

Наш менеджер должен принять важные решения в связи с выходом новой книги. Он должен определить тираж книги, установить уровень рекламы и назначить цену, точнее коэффициент надбавки по отношению к себестоимости книги. А целью менеджера, является, естественно, получение максимального дохода от выпуска книги.

Дадим имена параметрам, которыми может управлять менеджер: Тир, Рек и Цен. Менеджер хотел бы подобрать их значения так, чтобы оптимизировать доход от выпуска книги. Для начала он решил ограничиться тремя возможными вариантами (сценариями). Приведем их названия и соответствующие значения параметров:

Сценарий(1). МинимальныйТираж - (Тир = 5000, Рек = 0, Цен = 1,5)Сценарий(2). НормальныйТираж - (Тир = 10000, Рек = 2, Цен = 2)Сценарий(3). МаксимальныйТираж - (Тир = 30000, Рек = 5, Цен = 2,5)

Рассмотрим теперь, как доход связан с параметрами, управляемыми менеджером. Конечно, можно было бы написать совсем простую функцию. Чтобы научиться работать со сценариями, вид функции не важен. Но мы усложним задачу и напишем нечто правдоподобное. Доход зависит от продаж, а чтобы их прогнозировать, желательно иметь соответствующую модель. Наш менеджер уже построил модель продаж для среднесрочных прогнозов. Но сейчас ему нужна общая модель, подходящая для полного (годового) цикла продаж. Обобщая данные по продажам выпущенных книг, менеджер построил такую модель и получил соотношение, позволяющее рассчитать ожидаемое количество проданных книг в каждом месяце в течение года с момента выхода книги. Вот общий вид этого соотношения:

Продажи книг =a0+a1*t+a2*t^2+a3*Рек+a4*Кон*Цен

Зависимость продаж книги во времени можно описать квадратичным полиномом с отрицательным коэффициентом a2 при t^2. Это соответствует тому, что вначале спрос на книгу растет, достигает пика на рассматриваемом временном интервале и идет на убыль. Но на спрос влияют и другие факторы. Так, элемент a3*Рек отражает увеличение спроса, вызванное улучшением рекламы. Высокие надбавки на цену по отношению к себестоимости снижают спрос при наличии конкурирующих книг: коэффициент a4 всегда отрицательный. Оценки параметров a0, a1, a2, a3 и a4 менеджер получил по результатам измерений, используя функцию ЛИНЕЙН.

Второе ключевое соотношение связывает доход с количеством проданных книг с учетом произведенных затрат на их выпуск:

Доход = N * Цен * Себ - b1*Рек - b2*Тир*Себ -b3*T

Здесь N - это проданное количество книг, T - время продажи (в месяцах), Себ - себестоимость книги. Доход, согласно этому соотношению, зависит от количества проданных книг и той надбавки (Цен), которую менеджер решил установить на цену. Расходы определяются затратами на выпуск всего тиража, затратами на рекламу и затратами на продажу в течение периода T. Чтобы модель получила законченный вид, скажем, как считаются N и T.
N = min(Продажи книг(tI), Тир)
Это соотношение отражает тот очевидный факт, что при хорошем спросе весь тираж может быть распродан быстрее, чем за год, и тогда N совпадает с Тир. В случае неудачи за год будет продано N книг, возможно существенно меньше, чем полный тираж. Вместе с N считается и T - количество месяцев, за которое удалось распродать весь тираж. Заметьте, я не привожу соотношение для расчета T. Хотя алгоритм его расчета очевиден, его не удается описать одной формулой, и мне пришлось реализовать его программно отдельной процедурой с именем "ПериодПродаж", текст которой приведу чуть позже.

---

---