Циклические вычисления

Если зависимые ячейки Excel образуют цикл, то говорят, что имеют место циклические ссылки (circular references). В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя устранить циклические ссылки. Следуя обычной семантике, он не может провести вычисления, так как циклические ссылки порождают бесконечные вычисления. Есть два выхода из этой ситуации, - устранить циклические ссылки или изменить настройку в машине вычислений так, чтобы такие вычисления стали возможными. В последнем случае, естественно, требуется, чтобы число повторений цикла было конечным. Excel допускает переход к новой семантике, обеспечивающей проведение циклических вычислений. Вручную, для этого достаточно на вкладке Вычисления (меню Сервис, пункт Параметры) включить флажок Итерации и при необходимости изменить число повторений цикла в окошке "Максимум итераций". Можно также задать точность вычислений в окошке "Максимальное изменение", что также приводит к ограничению числа повторений

цикла. По умолчанию максимальное число итераций и точность вычислений соответственно имеют значения 100 и 0,0001. Понятно, что включить циклические вычисления и задать значения параметров, определяющих окончание цикла, можно и программно.

Укажем, особенности семантики циклических вычислений:

Формулы, связанные циклическими ссылками, вычисляются многократно. Запись формул на листе определяет порядок их вычисления. Формулы вычисляются сверху вниз, слева направо.Число повторений цикла определяется параметрами, заданными на вкладке Вычисления. Цикл заканчивается при достижении максимального числа итераций или, когда изменения значений во всех ячейках не превосходят заданной точности.

В каких же ситуациях требуется прибегать к циклическим вычислениям? Это, возможно, следует делать, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. У нас уже были примеры реализации итерационных процессов, например, вычисление суммы ряда, задающего экспоненту, в которых не применялись циклические ссылки. Платой за это было использование дополнительных ячеек таблицы Excel. Правда, появлялись и новые возможности, - возможность построить график, проанализировать процесс сходимости и т.д. Тем не менее, программисту, привыкшему к традиционным языкам, и привыкшему "с детства" экономить на переменных, может показаться странным предложенное решение задачи о нахождении корня уравнения, где на экран выводятся результаты всех приближений. В Excel экономия ячеек не главная задача. Тем не менее, при реализации итерационных процессов можно, конечно, и в Excel иметь одну единственную ячейку X, значение которой изменяется, начиная от начального прибли жения до искомого результата. Это в большей степени соответствует понятию переменной в языках программирования.

Циклические вычисления чисел Фибоначчи

Эта задача интересна тем, что она отчетливо демонстрирует ситуацию, когда начальный отрезок ряда чисел вычисляется по "своим" формулам и лишь, начиная с третьего числа, идут вычисления по рекуррентным соотношениям. Для того чтобы в каждый момент иметь не весь ряд вычисленных чисел, а только последние полученные значения, нам потребуются три ячейки таблицы Excel. Заметьте, двумя ячейками не обойтись. Формулы в двух первых ячейках используют конструкцию IF, позволяющую на первом шаге вычислений задать соответствующую константу, а затем перейти к рекуррентному соотношению. Третья ячейка необходима, как дополнительная память при пересылке значений. Для реализации задачи я выполнил следующие действия:

В ячейку Fprev занес IF - формулу: "=ЕСЛИ(Fprev=0; 1; Fib)"В ячейку Fib занес IF - формулу: "=ЕСЛИ(Fib=0; 1; Fnext)"В ячейку Fnext ввел формулу: "=Fprev + Fib"Эти формулы порождают на первом шаге вычислений тройку чисел (1,1,2), на втором - (2,3,5) и т.д.Напомним, что важен порядок расположения этих формул на рабочем листе. Они должны идти сверху вниз, слева направо.

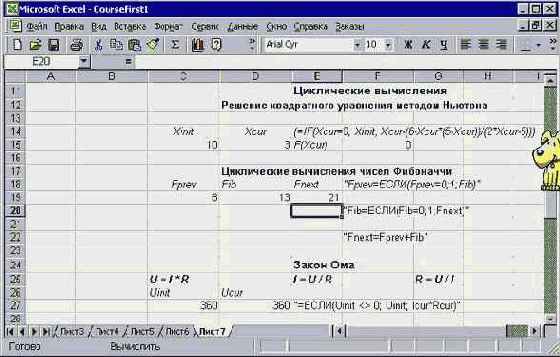
Взгляните, как выглядит на рабочем листе решение задач по нахождению корня уравнения и вычисления чисел Фибоначчи, использующее циклические вычисления.

увеличить изображение
Рис. 2.2. Циклические вычисления и итерационные процессы

Циклические вычисления и нахождение корней уравнения

Покажем, как можно использовать циклические вычисления на примере задачи нахождения корня уравнения методом Ньютона. Для простоты я начну с квадратного уравнения, а позже рассмотрю и более "серьезные" уравнения. Итак, рассмотрим квадратное уравнение: X2 -5X+6 =0. Найти корень этого (и любого другого уравнения) можно, используя всего одну единственную ячейку Excel. Для этого достаточно включить режим циклических вычислений и ввести в произвольную ячейку с именем, скажем X, рекуррентную формулу, задающую вычисления по Ньютону:

= X - F(X)/F1(X),

где F и F1 задают соответственно выражения, вычисляющие функцию и производную. Для нашего квадратного уравнения после ввода формулы в ней появится значение 2, соответствующее одному из корней уравнения. А как получить второй корень? Обычно, это можно сделать путем изменения начального приближения. В нашем случае начальное приближение не задавалось, итерационный процесс вычислений начинался со значения, хранимого в ячейке X по умолчанию и равного нулю. Как же задать начальное приближение в циклических вычислениях? Возникшая проблема не связана с данной конкретной задачей. Она возникает всегда в циклических вычислениях, - до начала цикла надо задать начальные установки. В рекуррентных соотношениях всегда есть некоторый начальный отрезок. Решать задачу задания начальных установок в каждом случае можно по-разному. Я продемонстрирую один прием, основанный на использовании функции ЕСЛИ. Вот как выглядит "настоящее" решение этой задачи, использующее 4 ячейки, две из которых нужны по существу дела, а две используются для повышения наглядности процесса вычислений:

В ячейку с именем Xinit я ввел начальное приближение.В ячейку Xcur, в которой и будет идти циклический счет, ввел формулу: = ЕСЛИ(Xcur =0; Xinit; Xcur - (6- Xcur *(5- Xcur))/(2* Xcur -5))В две другие вспомогательные ячейки я поместил текст этой формулы и формулу, задающую вычисление функции в точке Xcur, позволяющую следить за качеством решения.Заметьте, что на первом шаге вычислений, функция IF (ЕСЛИ) поместит в ячейку Xcur начальное значение, а затем уже начнет счет по формуле на последующих шагах.Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Xinit и запустить процесс вычислений. В этом случае вычисления будут продолжены, начиная с последнего вычисленного значения. Чтобы обнулить значение, хранящееся в ячейке Xcur, нужно заново записать туда формулу. Для этого достаточно выбрать ячейку и выделить текст формулы непосредственно в окне ее редактирования. Щелчок по Enter начнет вычисления с новым начальным приближением.

Функции с побочным эффектом и неявная передача данных

Возможность написать функцию с побочным эффектом или неявной передачей данных является одной из основных причин вычисления всех пользовательских функций при пересчете электронной таблицы. Давайте приведем примеры, проясняющие ситуацию. С этой целью я написал три функции:

ПравильнаяФункция( X As Variant) As Variant. Это пример хорошей, правильно построенной функции. Через параметр X ей передается значение некоторой ячейки рабочего листа (объект Range). В качестве результата она возвращает значение функции,- в нашем примере результат является копией входного параметра X.ПобочныйЭффект(X As Variant, Y As Variant) As Variant. В данной функции помимо вычисления результата изменяется и значение параметра Y. Поскольку по умолчанию параметр передается по ссылке (By Ref), то это должно было бы привести к побочному эффекту и изменить содержимое ячейки рабочего листа, переданной в качестве параметра Y. Мы увидим, что этого, однако, не происходит. НеявнаяПередача(X As Variant) As Variant В данной функции результат зависит не только от входного параметра X, но и от значения другой, неявно используемой ячейки рабочего листа.

Вот как выглядят описания наших функций:

Public Function ПравильнаяФункция(X As Variant) As Variant 'При вызове функции в формуле рабочего листа ей может быть передан объект 'Range - отдельная ячейка или диапазон. Возвращаемый результат 'также является объектом Range. Если передается и возвращается массив, 'то, естественно, функция должна вызываться в формуле над массивами.

ПравильнаяФункция = X End Function Public Function ПобочныйЭффект(X As Variant, ByRef Y As Variant) As Variant 'Также, как и ПравильнаяФункция данная функция возвращает 'в качестве результата переданный ей параметр X. ПобочныйЭффект = X

'Побочным эффектом является изменение параметра Y, переданного по ссылке. 'Однако заметьте, это изменение не затрагивает ячеек рабочего листа! Y = X

'Попытка явного изменения значений ячеек рабочего листа 'также не приводит к успеху. В этом случае и функция не возвращает 'правильный результат. Ее результат в этом случае - #ЗНАЧ. 'Range("C4") = 777

Const mes1 = "Если объект Range, переданный " Const mes2 = " в качестве второго аргумента функции ПобочныйЭффект" Const mes3 = " хранит значение, несовпадающее с первым аргументом, " Const mes4 = " то побочный эффект отсутствует!" MsgBox (mes1 & vbCrLf & mes2 & vbCrLf & mes3 & vbCrLf & mes4) End Function

Public Function НеявныеДанные(X As Variant) As Variant 'Передача данных из рабочего листа в функцию, 'минуя параметры, является возможной! Dim R As Range Set R = Range("C4") MsgBox ("В ячейке C4 хранится значение " & R.Value) НеявныеДанные = X.Value + R.Value End Function

Вот как выглядит рабочий лист Excel, на котором вызываются эти функции:

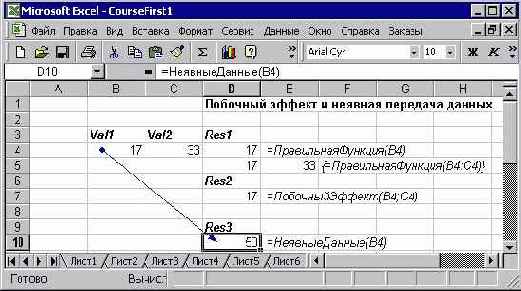
Рис. 2.1. Побочный эффект и неявная передача данных

Анализируя полученные результаты, обратим внимание на следующие моменты:

Функция, которую я назвал "ПравильнаяФункция", при вызове ее из рабочей формулы получает объект Range в качестве своего параметра X, и возвращает объект Range в качестве результата выполнения функции. Объект Range может быть единственной ячейкой, и в этом случае функция может вызываться в обычной рабочей формуле. Если же функция получает массив ячеек и возвращает массив, то она должна вызываться в формуле над массивами. На рабочем листе я продемонстрировал оба способа вызова функции. В ячейку D4 я записал формулу "=ПравильнаяФункция(B4)". Поскольку функция в качестве результата возвращает переданный ей аргумент, то значение, записанное ячейку D4, будет совпадать со значением 17, хранящемся в ячейке B4. Затем я в ячейки D5:E5 записал формулу над массивами "{=ПравильнаяФункция(B4:C4)}". В результате эта же функция позволяет скопировать диапазон ячеек.В функции ПобочныйЭффект, хотя Y и получает "правильное" значение переменной X, но это никак не сказывается на значении ячейки рабочего листа, переданной в качестве параметра Y, хотя параметр передается по ссылке. Так что можно полагать, что передача объектов Range рабочего листа Excel в функцию всегда происходит по значению, а не по ссылке.Всякая попытка явно или неявно изменить значения ячеек рабочего листа в процессе работы функции рабочего листа помимо возвращаемого функцией результата оканчивается неуспехом. Более того, попытка явно изменить значение в ячейке приводит к тому, что результат функции становится неопределенным. Так что побочный эффект во всех его проявлениях запрещен. Изменить содержимое листа можно только, возвращая результат работы вызываемых функций в формулах рабочего листа.В функции НеявныеДанные создается локальный объект Range. Он получает значение одной из ячеек рабочего листа, и это значение влияет на результат, возвращаемый функцией. Тем самым становится возможной неявная передача данных, минуя аппарат формальных параметров. Заметьте, что Excel не может обнаружить такой способ зависимости между ячейками. Мы специально отразили существующие, по мнению Excel зависимости. Как видите, Excel не подозревает, что ячейка D10 зависит от ячейки C4. Именно возможность неучтенных зависимостей заставляет Excel полностью проводить вычисления всех наличествующих пользовательских функций.Ни функции с побочным эффектом, ни функции с неявной передачей данных не вызывают никаких предупреждающих сообщений.

Const mes1 = "Если объект Range, переданный " Const mes2 = " в качестве второго аргумента функции ПобочныйЭффект" Const mes3 = " хранит значение, несовпадающее с первым аргументом, " Const mes4 = " то побочный эффект отсутствует!" MsgBox (mes1 & vbCrLf & mes2 & vbCrLf & mes3 & vbCrLf & mes4) End Function

Public Function НеявныеДанные(X As Variant) As Variant 'Передача данных из рабочего листа в функцию, 'минуя параметры, является возможной! Dim R As Range Set R = Range("C4") MsgBox ("В ячейке C4 хранится значение " & R.Value) НеявныеДанные = X.Value + R.Value End Function

Вот как выглядит рабочий лист Excel, на котором вызываются эти функции:

Инструментальное средство Excel - "Решатель"(Solver)

Для транспонирования, умножения и обращения матриц Excel имеет стандартные функции: ТРАНСП, МУМНОЖ и МОБР. Но в инструментарии Excel, доступном пользователю, есть более мощное средство, позволяющее в общем случае решать задачи нелинейного программирования, - Решатель (Solver). Как частный случай, он позволяет, например, найти решение нелинейных уравнений, которые рассматривались в задачах 3 и 4 предыдущей главы, и для решения которых я применял метод Ньютона. Частным случаем для Решателя является и решение систем линейных уравнений.

Общая постановка задачи

Задачи, которые можно решить с помощью Решателя, в общей постановке формулируются так:

Найти:

x1, x2, … xn

такие, что:

F(x1, x2, ….xn) -> {Max; Min; =Value}

при ограничениях:

GI(x1, x2, …xn) -> {<= Value; >= Value; = Value} I = 1…N

Искомые переменные - ячейки рабочего листа Excel - называются регулируемыми (adjustable) ячейками. Целевая функция F(x1, x2, …xn), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:

найти максимум целевой функции F(x1, x2, …xn);найти минимум целевой функции F(x1, x2, …xn);добиться того, чтобы целевая функция F(x1, x2, …xn) имела фиксированное значение: F(x1, x2, ….xn) = A.

Функции GI(x1, x2, …xn) называются ограничениями. Их можно задать как в виде равенств, так и неравенств. На регулируемые ячейки можно наложить дополнительные ограничения: положительности и/или целочисленности, тогда искомое решение ищется в области положительных и/или целых чисел.

Под эту постановку подпадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования. Такие задачи обычно проще сформулировать, чем решить. И иногда для решения конкретной оптимизационной задачи требуются специально для нее сконструированные методы. Решатель имеет в своем арсенале мощные универсальные методы решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ. Так что в более или менее простых случаях можно надеяться на успех. Кстати, помимо решения, делается и дополнительный анализ. Например, для задач линейного программирования делается анализ на чувствительность, позволяющий понять, насколько полученное решение нечувствительно к изменению ограничений. Предусмотрена и возможность управления процессом поиска решения.

Параметры, управляющие работой Решателя

Рассмотрим возможности управления работой Решателя, задаваемые в окне Параметры (Options):

Максимальное время (MaxTime) - ограничивает время, отведенное на процесс поиска решения. По умолчанию задано 100 секунд, что обычно достаточно для задач небольшой размерности, имеющих около 10 ограничений. Для задач большой размерности придется это значение увеличивать.Предельное число итераций (Iterations) - еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, но это число можно увеличивать до 32767. Чаще всего, если решение не получено за 100 итераций, надежд получить его при увеличении этого значения мало. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.Относительная погрешность (Precision) - задает точность выполнения ограничений. Иногда проще изменить ограничение, отодвинув границу, чем пытаться выполнить ограничения с высокой точностью.Сходимость (Convergence) - задается десятичной дробью, меньшей единицы, позволяя остановить процесс поиска при сходимости решения к неподвижной точке, когда относительные изменения в течение последних 5 итераций не превышают заданную дробь.Линейная модель (Assume Linear Model) - этот флажок следует включать, когда целевая функция и ограничения - линейные функции. Эта дополнительная информация позволяет Решателю упростить процесс поиска решения.Неотрицательные значения (Assume Non-Negative) - этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.Показывать результаты итераций (Show Iteration Results) - флажок, позволяющий включить пошаговый процесс поиска, показывая на экране результаты каждой итерации. В сложных ситуациях, когда Решатель не находит решения автоматически, рекомендуется включать этот флажок, так как иногда можно найти точку, от которой процесс поиска уклонился в сторону.Автоматическое масштабирование (Use Automating Scaling) - флажок автоматического изменения масштаба следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, задающая суммарную стоимость, измеряется в миллионах рублей.Относительная погрешность (Tolerance) - задается в процентах. Указанное значение имеет смысл только для задач с целочисленными ограничениями. Решатель в таких задачах вначале находит оптимальное не целочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более чем на указанное данным параметром количество процентов. Если такая точка найдена, Решатель сообщает об успехе. При большом допуске (по умолчанию 5%) может быть потеряно лучшее целочисленное решение, правда, отличающееся от найденного Решателем в пределах допуска. Для целочисленных задач допуск имеет смысл уменьшить, что я и сделал при решении транспортной задачи. Хочу еще раз обратить внимание на эту особенность решения задач целочисленного программирования. Если значение параметра Tolerance задать большим, то Решатель может остановиться раньше времени, не найдя лучшего целочисленного решения. Если же его взять малым, то наилучшее целочисленное решение будет отличаться от оптимального нецелочисленного решения на величину большую, чем ту, которая задается параметром Tolerance. В этом случае формально решение заканчивается неуспехом, поскольку найденное решение не удовлетворяет всем требованиям. Конечно, параметр Tolerance играет служебную роль, и "умный" Решатель, найдя наилучшее целочисленное решение, должен был бы уведомлять, что решение найдено, но ограничение по Tolerance не выполнено. Этого, однако, не происходит. Мы еще столкнемся с этой ситуацией при рассмотрении следующей задачи. Сохранить модель (Save Model) - командная кнопка; позволяет открыть диалоговое окно, где можно указать имя сохраняемой модели. Имеет смысл использовать эту возможность, когда на рабочем листе несколько моделей, так как единственная модель запоминается автоматически.Загрузить модель (Load Model) - позволяет загрузить одну из сохраненных моделей.Есть еще несколько более специальных параметров, которыми можно управлять, варьируя процедурами, применяемыми в процессе поиска. К ним следует прибегать в тяжелых ситуациях, когда решение найти не удается.

Пользовательские функции и массивы рабочего листа

Учитывая важность проблемы передачи массивов рабочего листа в пользовательскую функцию, кратко сформулируем основные выводы еще раз:

Пользовательская функция, вызываемая в формуле рабочего листа, может принимать один или несколько массивов в качестве своих входных параметров. Эти параметры должны иметь тип Variant.На выходе функция может сформировать только один массив, который можно передать в рабочий лист. Этот массив не может быть значением одного из параметров функции - только результатом этой функции, т. е. побочный эффект не допускается. Всякая попытка вызвать функцию с побочным эффектом обнаруживается динамически (но не в период трансляции) и приводит к ошибке при вычислении результата.Пользовательская функция, возвращающая массив рабочего листа, должна иметь тип Variant.

Ряд важных вопросов требует специального рассмотрения. Вот лишь некоторые:

Что собой представляют формулы, вызывающие пользовательские функции, когда те получают массивы рабочего листа как параметры, но их результатом является скаляр? Вызываются ли они как формулы с массивами или как обычные формулы?Я уже сказал, что в пользовательскую функцию можно передать массив рабочего листа, для чего необходимо, чтобы соответствующий формальный параметр имел тип Variant. Но Variant является универсальным типом, а посему можно передавать не только отдельные ячейки и массивы. Что можно передавать в качестве фактического параметра, как при этом построить обработку? Ответы на эти вопросы я дам при рассмотрении следующей задачи.

Пользовательские функции, принимающие сложный объект Range

Известно, что объект Range может представлять несмежную область и являться объединением нескольких интервалов ячеек. Иначе говоря, один объект Range может задавать несколько массивов рабочего листа. Можно ли такой объект передать пользовательской функции и, если да, то как его обрабатывать? Ответ: "можно", хотя соответствующий формальный параметр следует описывать особым образом. Процедуры и функции VBA допускают произвольное число параметров, это достигается за счет того, что один, последний по счету формальный параметр может иметь спецификатор ParamArray. В этом случае данный параметр задает фактически массив параметров с произвольным числом элементов. Именно эта техника и применяется для передачи в пользовательскую функцию сложного объекта Range, представляющего не один, а произвольное число массивов. У такой функции последний параметр должен иметь спецификатор ParamArray и быть массивом типа Variant.

Рассмотрим предыдущую задачу, немного усложнив ее, полагая, что при проверке кандидата на "медианность" используется произвольное число массивов. Вот как выглядит функция, решающая эту задачу:

Public Function IsMedianaForAll(Cand As Variant, _ ParamArray M() As Variant) As Integer 'Эта функция осуществляет те же вычисления, что и функция IsMediana 'Важное отличие состоит в том, что аргумент M может быть 'задан сложным объектом Range 'или представлять объединение массивов. Dim Pos As Integer, Neg As Integer Pos = 0: Neg = 0 Dim Elem As Variant For Each Elem In M 'Анализ типа параметра Elem If TypeName(Elem) = "Range" Then For i = 1 To Elem.Rows.Count For j = 1 To Elem.Columns.Count If Elem.Cells(i, j) > Cand Then Pos = Pos + 1 ElseIf Elem.Cells(i, j) < Cand Then Neg = Neg + 1 End If Next j Next i

ElseIf TypeName(Elem) = "Variant()" Then 'TypeName is "Variant()" 'Это массив, но для него, к сожалению, не всегда корректно работают, 'например, функции границ: LBound, UBound. Dim Val As Variant For Each Val In Elem If Val > Cand Then Pos = Pos + 1 ElseIf Val < Cand Then Neg = Neg + 1 End If Next Val Else MsgBox ("При вызове IsMedianaForAll один из аргументов" & _ vbCrLf & "не является массивом или объектом Range!") End If Next Elem IsMedianaForAll = Pos - Neg

End Function

Комментируя работу этой функции, отмечу:

Формально эта функция по- прежнему имеет два параметра Cand и M. Правда, теперь они поменялись местами, и параметр M стал последним. Фактически у этой функции теперь произвольное число параметров, поскольку параметр M, сохранив тип Variant, стал массивом параметров. Спецификатор ParamArray подчеркивает, что это специальный массив с произвольным числом элементов.Для работы с массивом M используется цикл типа For Each. В цикле выделяется очередной элемент Elem типа Variant, а дальше используется уже знакомый по функции IsMediana алгоритм проверки элемента Cand.Разбор случаев делается независимо для каждого из элементов массива M. Это значит, что на входе могут быть заданы одновременно как массивы рабочего листа, так и массивы констант Visual Basic.

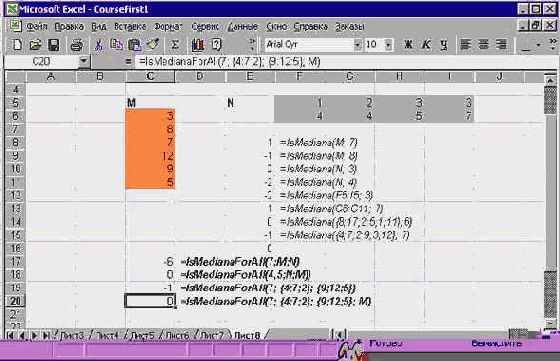
На том же рабочем листе, где проводились эксперименты с формулами, вызывающими функцию IsMediana, я записал еще несколько формул, вызывающих функцию IsMedianaForAll. В этих формулах аргумент может иметь сложный вид, допуская, по существу, сколь угодно большое число параметров.

увеличить изображение
Рис. 2.6. Вызов функции IsMedianaForAll, допускающей сложные объекты Range

Проанализируем четыре сделанных вызова:

=IsMedianaForAll(7;M;N). В этом вызове наш кандидат - число 7 - проверяется по отношению к объединению двух массивов рабочего листа, заданных своими именами M и N. Формальных параметров у функции два, а фактических при вызове задается три. Два последних можно рассматривать как сложный объект Range, представляющий несмежную область ячеек, задающую объединение вектора M и матрицы N. С программистской точки зрения, можно полагать, что передается массив с произвольным числом элементов, где каждый из них в свою очередь является массивом. Такой фактический параметр является допустимым значением формального параметра нашей функции, имеющего спецификатор ParamArray.=IsMedianaForAll(4,5;N;M). В этом вызове мало нового в сравнении с предыдущим. Изменен порядок следования массивов N и M, изменен кандидат, - им стало число 4.5, не входящее ни в один из массивов. Как показывает результат, это число является медианой объединенных массивов.=IsMedianaForAll(7; {4;7;2}; {9;12;5}). Здесь в роли аргументов выступают массивы Visual Basic, заданные в виде констант, заключенных в фигурные скобки. Фактическое значение параметра M в этом случае представляет массив из двух элементов, каждый из которых в свою очередь является массивом.=IsMedianaForAll(7; {4;7;2}; {9;12;5}; M). Ситуация в этом вызове сложнее, так как число аргументов возросло, но, что более важно, среди них есть как массивы Visual Basic, так и массив рабочего листа - вектор M. Тем не менее, все работает правильно.

"Пользовательские" и "обычные" функции VBA

Под пользовательской функцией VBA я понимаю функцию, которая может быть вызвана в формулах рабочего листа Excel. Обычные функции VBA могут вызываться в функциях и процедурах VBA. Возникает естественный вопрос, может ли одна и та же функция одновременно быть пользовательской и обычной? Этот же вопрос может быть сформулирован и по-другому, есть ли особая специфика в пользовательских функциях? Ответ прост - особой специфики нет, и одна и та же функция может вызываться как в формулах, так и в процедурах VBA. Практически не возникает проблем, когда аргументами функции и результатом являются скалярные значения. Когда же, как в случае с MultMatr, аргументами и результатом являются массивы, то возникают определенные трудности. Эти трудности преодолимы, примером тому служит функция MultMatr. Попробуем разобраться, в чем состоят эти трудности. Когда функции нужно предать массив, то в пользовательских функциях при вызове им передаются объекты Range, обычным функциям - пер еменные, описанные, как массивы VBA. Поэтому для обеспечения универсального характера функции в ее теле необходимо производить разбор случаев, определяя тип параметра. В результате растет объем функции, а, следовательно, усложняется ее понимание. Еще одна сложность связана с результатом вычислений. Никаких проблем нет для формулы над массивами, вызывающей пользовательскую функцию, - результат, записывается в область, выделенную при вызове формулы. Обычные функции VBA, как правило, не возвращают массив в качестве результата. Если результатом работы является массив, то при программировании на VBA создается процедура, а не функция. Дело в том, что в VBA присваивания над массивами запрещены, потому просто невозможно присвоить массиву значение обычной функции, возвращающей массив в качестве своего результата. Как же, спросите Вы, MultMatr может использоваться в качестве обычной функции? Только за счет маленьких хитростей и универсального типа Variant, который может быть чем угодно, в том числе и массивом. При вызове MultMatr как обычной функции в процедуре VBA результат вызова присваивается переменной типа Variant, - это допустимо. Затем уже с этой переменной можно работать как с массивом, - это тоже допустимо, что я и продемонстрирую чуть позже. Таким образом, всегда можно написать функцию так, чтобы она служила и как пользовательская и как обычная функция. Другой вопрос, стоит ли это делать. В таком обобщении есть свой резон, поскольку в таких случаях при вызове пользовательской функции ей можно передавать в качестве аргументов не только объекты Range, но и массивы констант, что было продемонстрировано при рассмотрении функции IsMedianaForAll. Заметьте, однако, что в функцию MultMatr передать массивы констант невозможно. Причина этого в том, что для двумерных массивов констант функции UBound и LBound работают некорректно.

Подводя итог, замечу, что, когда приходится работать с массивами, разумнее иметь два варианта - пользовательскую и обычную функцию. Чтобы отчетливее продемонстрировать разницу между обычными и пользовательскими функциями, я написал обычную процедуру MultMatr1, выполняющую умножение матриц. Вот ее текст:

Public Sub MultMatr1(A() As Variant, B() As Variant, C() As Variant) 'Умножение матриц. 'Процедуру можно вызывать в обычных VBA функциях и процедурах, 'передавая ей в качестве параметров массивы VBA. Dim i As Integer, j As Integer, k As Integer Dim N As Integer, M As Integer, Q As Integer Dim P As Integer, NC As Integer, PC As Integer Dim msg1 As String, msg2 As String Dim Uncor1 As Boolean, Uncor2 As Boolean Dim Elem As Variant Uncor1 = True: Uncor2 = True msg1 = " При вызове MultMatr некорректно задана размерность" _ & " перемножаемых матриц!" & vbCrLf & _ "Число столбцов матрицы A = " & M & vbCrLf & _ "Число строк матрицы B = " & Q msg2 = " При вызове MultMatr некорректно задана размерность" _ & " матрицы результата!" & vbCrLf & _ "Число строк матрицы C = " & NC & vbCrLf & _ "Число столбцов матрицы C = " & PC

'Проверка корректности задания размерности N = UBound(A, 1): M = UBound(A, 2) Q = UBound(B, 1): P = UBound(B, 2) NC = UBound(C, 1): PC = UBound(C, 2) If (Q = M) Then ' Размерность исходных матриц задана корректно Uncor1 = False If NC = N And PC = P Then 'Размерность результата задана корректно Uncor2 = False 'Построение произведения матриц AB =A*B For i = 1 To N For j = 1 To P Elem = 0 For k = 1 To M Elem = Elem + A(i, k) * B(k, j) Next k C(i, j) = Elem Next j Next i Else 'некорректно задана размерность If Uncor1 Then MsgBox (msg1) If Uncor2 Then MsgBox (msg2) End If End If End Sub

От функции MultMatr она отличается тем, что в ней опущен разбор случаев и проводится более тщательная проверка корректности размерностей аргументов. Конечно, она ни в коем случае не может быть использована как пользовательская функция, но зато работать с ней в процедурах и функциях VBA с ней не то чтобы проще, но естественнее. Чтобы почувствовать разницу, я продемонстрирую тестовую процедуру, в которой вызываются, как функция MultMatr так и процедура MultMatr1.

Public Sub MultTest() Dim A(1 To 2, 1 To 2) As Variant Dim B(1 To 2, 1 To 2) As Variant Dim C(1 To 2, 1 To 2) As Variant Dim C1 As Variant Dim item As Variant Dim i As Integer, j As Integer A(1, 1) = 1: A(1, 2) = 2: A(2, 1) = 3: A(2, 2) = 4 B(1, 1) = 1: B(1, 2) = 2: B(2, 1) = 3: B(2, 2) = 4 'Переменной типа Variant присваивается массив C1 = MultMatr(A, B) For i = 1 To UBound(C1, 1) For j = 1 To UBound(C1, 2) Debug.Print C1(i, j) Next j Next i 'Здесь С - массив и работаем с ним, как с массивом. Call MultMatr1(A, B, C) For i = 1 To UBound(C, 1) For j = 1 To UBound(C1, 2) Debug.Print C(i, j) Next j Next i 'Вызов тестовой функции, возвращающей массив. C1 = ResArray(A) For Each item In C1 Debug.Print item Next item End Sub

Public Function ResArray(A() As Variant) As Variant 'Возвращает в качестве результата, 'переданный ей массив ResArray = A End Function

Как видите, функция MultMatr, успешно работающая в роли пользовательской функции, с тем же успехом может выполнять и роль обычной функции. Так что я выполнил поставленную задачу, создав "универсальную" функцию. Но, возможно, предпочтительнее в процедурах VBA работать с MultMatr1, не прибегая к переменным типа Variant. Обратите внимание на небольшую тестовую функцию ResArray, которую я написал, чтобы в явной форме продемонстрировать способ возвращения массива в функциях VBA.

Решатель и программирование

Правильная постановка оптимизационной задачи, грамотное использование Решателя требует от пользователя определенной математической культуры. В ряде случаев эту часть работы следует взять на себя программисту и организовать программный вызов Решателя, оставив за пользователем задание исходных данных. Все, что можно сделать вручную, можно сделать и на VBA и даже несколько больше, используя стандартный набор функций VBA для работы с Решателем. Кратко охарактеризую четыре основные функции:

SolverOk(SetCell, MaxMinVal, ValueOf, ByChange) - позволяет поставить задачу оптимизации. Она выполняет работу, эквивалентную установке параметров в диалоговом окне при вызове Решателя. Параметр SetCell задает ячейку, содержащую формулу с целевой функцией. Три возможных значения параметра MaxMinVal указывают, что с ней делать (максимизировать, минимизировать или пытаться зафиксировать ее значение, которое при этом задается параметром ValueOf). Последний по счету параметр ByChange задает диапазон регулируемых ячеек - переменных оптимизационной задачи.SolverAdd(CellRef, Relation, FormulaText) - позволяет добавлять ограничения в модель. Первый параметр CellRef задает левую часть ограничения в виде ссылки на ячейку или их диапазон. Пять возможных значений параметра Relation (1…5) определяют отношение, связывающее левую и правую часть ограничения (<=, =, >=, int, bin). Два последних отношения накладывают на переменные ограничения целочисленности и двоичности. Двоичные переменные могут принимать только два значения 0 и 1. Параметр FormulaText задает правую часть ограничений, он не должен задаваться, если отношение задано как int или bin.SolverOptions(MaxTime, Iterations, Precision, AssumeLinear, StepThru, Estimates, Derivates, Search, IntTolerance, Scaling, Convergence, AssumeNonNeg) - используя эту функцию, можно установить параметры Решателя, которые вручную устанавливаются в окне Options. Мы не будем их описывать, так как большинство из них мы фактически рассмотрели. Но на одном из них остановимся. Булев параметр StepThru имеет значение True, если включается пошаговое исполнение с прерыванием после выполнения каждой итерации. При программировании можно передать Решателю макрос, который будет выполняться при каждом таком прерывании.SolverSolve(UserFinish, ShowRef) - запускает Решатель. Ее действие эквивалентно выбору кнопки Solve. Возможный булев параметр UserFinish равен True, если результаты не выводятся на дисплей. Если параметр опущен или равен False, результаты появятся в диалоговом окне Решателя, предназначенном для их вывода. Параметр ShowRef представляет строку, задающую имя макроса, который должен выполняться в паузах между итерациями. Он задается, только если параметр StepThru равен True.

Решение систем линейных уравнений, умножение и обращение матриц

Задачи, перечисленные в заголовке, возникают достаточно часто в различных сферах деятельности, требующих применения математического аппарата. По этой причине в библиотеке Excel есть встроенные функции, позволяющие решить эти задачи. О встроенных функциях умножения матриц МУМНОЖ (MMULT) и транспонирования матриц МТРАНСП (MTRANSP) я уже упоминал, есть и функция для нахождения обратной матрицы - МОБРАТ (MINVERSE). Зная обратную матрицу и умея умножать матрицы, найти решение системы уравнений не представляет труда. Но поскольку умение решать эти задачи входит в круг начального образования программиста, то я полагаю уместным рассмотреть создание собственных аналогов этих функций на VBA. Заодно это позволит рассмотреть некоторые важные моменты в создании пользовательских функций, вызываемых в формулах рабочего листа. Многое мы уже знаем. Знаем, как написать пользовательскую функцию, какие ограничения накладываются на ее параметры с тем, чтобы ее можно было вызывать из формул рабочего листа Excel, передавая ей в качестве фактических параметров массивы рабочего листа. Знаем, как анализировать тип переданных данных. Знаем, как такая функция может вернуть массив и изменить содержимое рабочего листа. В последующих примерах я еще раз коснусь всех этих вопросов, а, кроме того, появятся и другие вопросы, на которые стоит обратить внимание.

Решение системы линейных уравнений методом простой итерации

Циклические вычисления можно проводить и над массивами. В качестве примера такой задачи рассмотрим итеративный способ решения системы линейных уравнений AX = B. Если применить метод простой итерации, то вектор решений X определяется следующим рекуррентным соотношением:

XK+1 = XK -(AXK -B) k= 1…N

Чтобы запустить процесс вычислений, нужно задать начальное приближение - вектор X1. Для сходимости процесса необходимо, но не достаточно, чтобы норма матрицы А была меньше 1. Иногда достаточно соответствующим образом масштабировать матрицу А и вектор В. Но нас конечно интересуют другие вопросы,- как реализовать на Excel это итеративное соотношение над векторами и матрицами, не прибегая к программированию на VBA и используя циклические вычисления. Покажем, что решение получить ненамного сложнее, в сравнении с применением схемы Ньютона для одного уравнения. Я сделал следующее:

Ввел матрицу А и вектор В, предварительно нормировав их. Заметим, что нужно правильно выбирать ориентацию векторов. В данном случае мне было удобнее представлять вектор В строкой. Вектор получил имя Veb.

Затем определил вектор с именем Vxinit, задающий начальное приближение.

Затем определил еще один вектор с именем Vxcur. Это вектор решений, его значения будут изменяться в цикле, пока не закончится итерационный процесс. Формула для вычислений будет определяться написанным выше рекуррентным соотношением, и представлять собой формулу над массивами. Учитывая то, что говорилось ранее о рекуррентных соотношениях, формула должна быть IF - функцией. Это позволит использовать на первом шаге начальное приближение, а потом уже вести вычисления по рекуррентной формуле. Приведем теперь саму формулу над массивами, вычисляющую рекуррентно вектор Vxcur:

{=ЕСЛИ(Vxcur=0; Vxinit; Vxcur - Axhor + Veb)}

Здесь, как и ранее, используются нулевые значения, как признак начала процесса. Заметим, что, конечно, было бы лучше, если бы существовала возможность явной инициализации переменных при циклических вычислениях, а так наши действия немного напоминают фокус. Вектор Axhor, введенный в формулу - это вспомогательный вектор, равный произведению матрицы А на текущий вектор Vxcur. Если процесс вычислений сходится, и Vxcur сходится к решению системы уравнений, то вектор Axhor будет сходиться к вектору Veb.

Опишем подробнее формирование вспомогательного вектора Axhor. Содержательно, он представляет произведение матрицы на вектор. Но произведение матрицы на вектор дает вектор столбец, а в рекуррентном соотношении необходим вектор строка. По этой причине я формирую вначале вектор столбец Axver:
Axver = A*Vxcur
Конечно, для умножения матрицы на вектор можно воспользоваться стандартной функцией, но я хочу показать, как это делается с использованием более простых средств. Для этого достаточно написать формулу, вычисляющую его первый элемент:
{=SUM(A38:B38*Vxcur)}
и затем скопировать ее по столбцу. Обратите внимание, вектор, на который умножается матрица, должен быть строкой, а вектор - результат - столбцом. Строка матрицы задается в относительных адресах и при копировании меняется. Вектор, на который умножаются строки, задается своим именем, а значит абсолютным адресом, не изменяющимся при копировании. Каждая формула, задающая элемент вектора, является формулой над массивами.

Получив вектор столбец Axver, задающий нужное произведение, можно перейти к получению строки - Axhor, представляющей результат транспонирования вектора Axver. Для транспонирования я использовал стандартную функцию Transpose. Сама задача транспонирования и эта функция подробно будет рассмотрена чуть позже. Формула над массивами, определяющая вектор Axhor имеет вид:
{=ТРАНСП(Axver)}
Задав все вектора и все формулы, я получил решение системы линейных уравнений. Как ни странно, но даже столь плохой метод, как метод простой итерации сошелся к решению. Так, начав с начального приближения (1,1), я получил решение (1.6, 2.4) с заданной точностью.

Заметим, предложенная схема носит общий характер и позволяет решать любую систему линейных уравнений, не ограничиваясь системой из двух уравнений, рассмотренную в примере. Однако никому не рекомендую применять метод простой итерации для нахождения решения системы уравнений, - для этого есть другие точные методы. Просто мне было важно продемонстрировать возможность циклических вычислений при действиях с матрицами, и нужен был достаточно простой пример.

В заключение темы о циклических вычислениях покажем, как выглядят построенное решение на рабочем листе Excel:

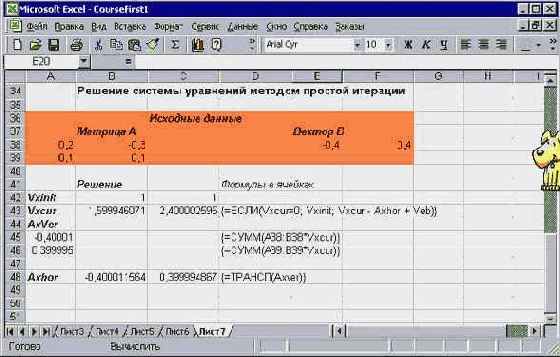
увеличить изображение
Рис. 2.3. Циклические вычисления и действия над матрицами

Опишем подробнее формирование вспомогательного вектора Axhor. Содержательно, он представляет произведение матрицы на вектор. Но произведение матрицы на вектор дает вектор столбец, а в рекуррентном соотношении необходим вектор строка. По этой причине я формирую вначале вектор столбец Axver:
Axver = A*Vxcur
Конечно, для умножения матрицы на вектор можно воспользоваться стандартной функцией, но я хочу показать, как это делается с использованием более простых средств. Для этого достаточно написать формулу, вычисляющую его первый элемент:
{=SUM(A38:B38*Vxcur)}
и затем скопировать ее по столбцу. Обратите внимание, вектор, на который умножается матрица, должен быть строкой, а вектор - результат - столбцом. Строка матрицы задается в относительных адресах и при копировании меняется. Вектор, на который умножаются строки, задается своим именем, а значит абсолютным адресом, не изменяющимся при копировании. Каждая формула, задающая элемент вектора, является формулой над массивами.

Получив вектор столбец Axver, задающий нужное произведение, можно перейти к получению строки - Axhor, представляющей результат транспонирования вектора Axver. Для транспонирования я использовал стандартную функцию Transpose. Сама задача транспонирования и эта функция подробно будет рассмотрена чуть позже. Формула над массивами, определяющая вектор Axhor имеет вид:
{=ТРАНСП(Axver)}
Задав все вектора и все формулы, я получил решение системы линейных уравнений. Как ни странно, но даже столь плохой метод, как метод простой итерации сошелся к решению. Так, начав с начального приближения (1,1), я получил решение (1.6, 2.4) с заданной точностью.

Заметим, предложенная схема носит общий характер и позволяет решать любую систему линейных уравнений, не ограничиваясь системой из двух уравнений, рассмотренную в примере. Однако никому не рекомендую применять метод простой итерации для нахождения решения системы уравнений, - для этого есть другие точные методы. Просто мне было важно продемонстрировать возможность циклических вычислений при действиях с матрицами, и нужен был достаточно простой пример.

В заключение темы о циклических вычислениях покажем, как выглядят построенное решение на рабочем листе Excel:

увеличить изображение
Рис. 2.3. Циклические вычисления и действия над матрицами

Транспортная задача

В офисной деятельности очень часто приходится анализировать варианты, стараясь найти оптимальное решение. К сожалению, математические методы оптимизации в реальной офисной практике применяются сравнительно редко. Причины этого я обсуждать здесь не буду. Наша цель другая, - показать, как решаются такие задачи. Поэтому я подробно останавливаюсь на возможностях Решателя, полагая, что это средство Excel позволяет легко и просто решать самые разные оптимизационные задачи, возникающие в ходе офисной деятельности.

Рассмотрим более серьезную оптимизационную задачу - транспортную. Вот одна из возможных содержательных постановок этой задачи:

Имеется N складов, на каждом из которых хранится готовая продукция. Пусть:

P1, P2, …PN

- объемы продукции, хранящейся на каждом складе. Пусть теперь есть M магазинов, от которых поступила заявка на завоз этой продукции:

Q1, Q2, …QM

- требуемые объемы продукции для каждого магазина. Транспортные расходы на перевозку единицы продукции из склада I в магазин J задаются матрицей:

|| TI,J || I = 1…N; J = 1…M

Требуется найти оптимальный план перевозок,- матрицу ||XI,J||, минимизирующую суммарные транспортные расходы при естественных ограничениях: все заявки магазинов должны быть удовлетворены, и со склада нельзя увезти продукции сверх того, что там имеется. В формальной постановке эта задача имеет вид:

XI,J* TI,J -> Min I J

При ограничениях:

XI,J <= PI I = 1…N; J

XI,J = QJ J =1…M; I

XI,J > = 0; I = 1…N; J = 1…M;

В качестве примера я рассмотрел транспортную задачу для 2 складов и 5 магазинов.

В ячейки C4:C5 записал объемы продукции, имеющиеся на 2 складах.В ячейки E5:I5 - заявки на продукцию, поступившие от магазинов.В ячейки B8:F9 - матрицу транспортных расходов, задающую расходы на перевозку из I-го склада в J-й магазин единицы продукции.В ячейки B13:F14 - план перевозок - матрицу, задающую количество товара, перевезенного из I-го склада в J-й магазин. Начальное распределение плана задано по принципу "каждой сестре по серьге", равномерно распределив всю имеющуюся на складе продукцию по магазинам. Эти ячейки являются регулируемыми и Решатель должен найти более подходящее решение, изменив значения в этих ячейках.В ячейку D15 - записал целевую функцию: {=СУММ(B8:F9*B13:F14)}В ячейки D17:H17 записал ограничения, задающие требование о точном выполнении заявки каждого магазина. Как обычно, я записал соответствующую формулу в первую из этих ячеек: {=СУММ(B13:B14) - E5}

Затем скопировал ее. При копировании формула автоматически меняется, задавая нужное ограничение. Правда, нужно следить при этом за правильной ориентацией данных. Например, в данном случае формулу нужно копировать в строку, а не в столбец.Затем задал следующую группу ограничений. Эти ограничения отвечают тому естественному условию, что со склада нельзя увести больше продукции, чем там имеется. Формула, помещенная в ячейку D18, имеет вид: {= С4 - СУММ(B13:F13)}

Эта формула скопирована уже по столбцу в ячейку D19. Подготовительный этап завершен - можно вызывать Решатель.

При вызове Решателя и задании параметров в его диалоговом окне выполнялась стандартная работа по указанию ячейки с целевой функцией, диапазоном регулируемых ячеек и заданием ограничений. Заметьте, помимо двух групп ограничений я задал и ограничения целочисленности переменных. Предполагается, что продукция может перевозиться только целыми единицами - бочками, мешками, ящиками. Такие ограничения в Решателе создаются совсем просто, - достаточно среди операторов, связывающих левую и правую части ограничения, выбрать оператор int. Взгляните, как выглядят результаты моей работы:

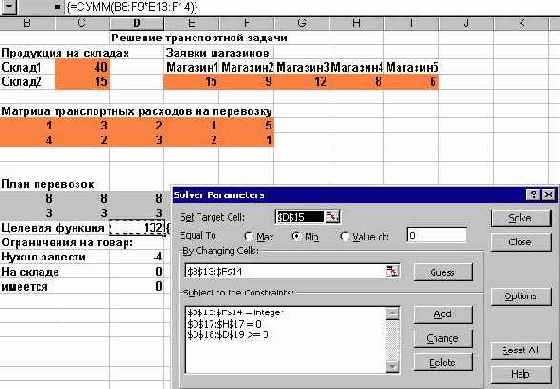
увеличить изображение
Рис. 2.21. Окно Решателя при решении транспортной задачи

Прежде чем дать команду на решение задачи, я провел настройку параметров в окне Options. В частности я включил флажки, указывающие на линейность модели и положительность переменных. Кроме того, я увеличил точность решения целочисленной задачи, задав в окне Tolerance значение в 1% вместо 5%, принятых по умолчанию.

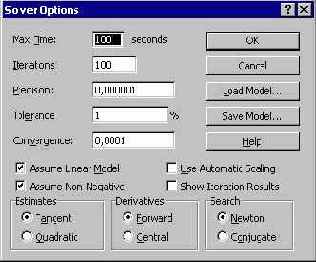
Рис. 2.22. Настройка в окне параметров Решателя при решении транспортной задачи

Осталось щелкнуть кнопку "Solve" и получить оптимальный план перевозок. Вы можете проанализировать, насколько оптимальный план отличается от равномерного распределения, предложенного в качестве первоначального варианта, и как уменьшились транспортные расходы:

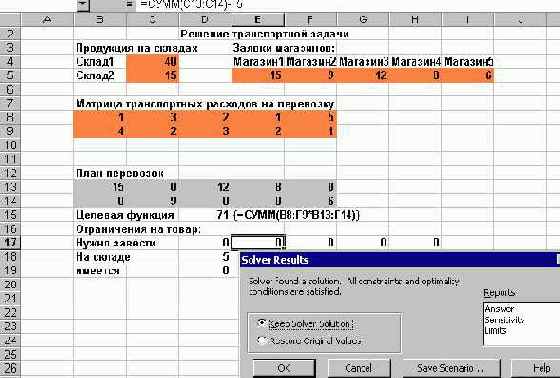
увеличить изображение
Рис. 2.23. Решение транспортной задачи

Задача 9 Транспонирование матриц

Постановка задачи: Транспонировать матрицу A: B= AT

Наша конкретная задача - транспонирование матрицы на новое место - решается сравнительно просто, поскольку для этого есть стандартная функция ТРАНСП(X). В английской версии и при программировании на VBA она называется Transpose. Можно, например:

ввести прямоугольную матрицу в область рабочего листа, скажем, в ячейки B34:D35;дать имя этой области, например, "MatrixA";выделить область ячеек с другой ориентацией для транспонированной матрицы, например A37:B39;ввести в эту область формулу над массивами: "{=ТРАНСП(MatrixA)}"

Можете убедиться, эти действия приводят к желаемому результату:

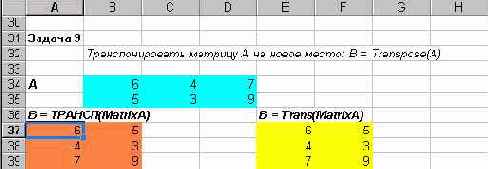
Рис. 2.4. Два решения в задаче транспонирования матрицы

Хорошо, что есть функция ТРАНСП. Но можно ли справиться с этой классической задачей, не прибегая к вызову стандартной функции? Эта задача имеет различные вариации: матрица может быть квадратной или прямоугольной, транспонировать ее можно на месте (для квадратных матриц) или получать результат, как новую матрицу. При транспонировании на месте возникают циклические ссылки, для прямоугольных матриц появляется проблема различной ориентации исходной матрицы и результата. Но даже в самом простом случае транспонирования квадратной матрицы на новое место при построении собственного решения написать одну или несколько формул в ячейках рабочего листа, решающих эту задачу для матриц произвольного размера, не удается. В отличие от приведенного в предыдущей главе примера с сигнальной матрицей здесь требуется оперировать с индексами элементов, а формулы над массивами этого не допускают. Выход в том, чтобы написать подобную функцию на VBA, вызов которой приведет к желаемому эффекту. Давайте создадим собственную функцию Trans, работающую, как и стандартная функция ТРАНСП. У функции Trans один аргумент. При вызове в качестве фактического параметра ей передается массив рабочего листа (объект Range), заданный в виде диапазона ячеек или своим именем. Этот массив (прямоугольная матрица) транспонируется, и новая матрица возвращается как результат. Она должна быть записана в выделенную в момент вызова область ячеек, отведенных для транспонированной матрицы. Функция Trans, как и функция ТРАНСП, должна вызываться в формуле над массивами и, следовательно, связывается с каждой ячейкой выделенной области.

Итак, с программистской точки зрения, нам нужно написать функцию от одного параметра, тип которого должен допускать при вызове массивы рабочего листа (объекты Range) и такой же массив возвращать как результат функции. Каким же должен быть тип параметра и тип функции? Если Вы внимательно следили за предыдущими примерами, то понимаете, что таковым является тип Variant - этот универсальный тип успешно работает в данной ситуации. Остальное - дело техники. Вот текст функции Trans, решающий нашу задачу:

Public Function Trans(A As Variant) As Variant 'Функция предназначена для транспонирования массивов 'рабочего листа Excel - объектов Range. 'При работе с переменной A используются свойства объекта Range

Dim B() As Variant Dim i As Integer, j As Integer 'Динамическому массиву В выделяется память ReDim B(1 To A.Columns.Count, 1 To A.Rows.Count) As Variant For i = 1 To A.Rows.Count For j = 1 To A.Columns.Count B(j, i) = A.Cells(i, j) Next j Next i 'Массив B возвращается в качестве результата функции Trans. Trans = B End Function
Нам остается сделать несколько замечаний:
Параметр и функция имеют тип Variant, согласуемый как с массивом, так и объектом Range.Чтобы получить транспонированную матрицу, нам понадобился динамический массив B. Оператор ReDim в процедуре Trans позволяет массиву получить память, - его размеры можно определить, зная свойства объекта Range, задающего входной массив A.Операция транспонирования реализуется двойным циклом.На последнем шаге работы функции ее значением становится сформированный массив B. Он и будет записан в выделенную область памяти рабочего листа.
Заметьте, на предыдущем рисунке показаны оба варианта решения задачи транспонирования матрицы с использованием стандартной функции ТРАНСП и собственной функции Trans.
Хочу еще раз обратить внимание на то, чего делать нельзя. Например, в данной задаче многим программистам хотелось бы получать результат в качестве побочного эффекта, введя функцию:
ТрансТакНельзя(A As Variant, B As Variant) As Boolean
Эта функция получала бы два массива A и B - входной и результирующий. Транспонированная матрица (массив B) получалась бы как побочный эффект. Результатом работы функции могло бы быть значение True в случае успеха работы и False в противном случае. Такая схема, возможная в других языках и в том числе на VBA недопустима, когда функция вызывается в Excel. Пользовательские функции, вызываемые в формулах ячеек рабочего листа, не допускают побочного эффекта, приводящего к изменению массивов на рабочем листе. Единственная возможность - передать массив как результат пользовательской функции, вызываемой в формуле над массивами. Об этой особенности Excel я уже говорил ранее, но не грех напомнить еще раз об этой важной специфике машины вычислений Excel.

Задача 10 Нахождение медианы

Постановка задачи: Для массива M и элемента Cand вычислить разность между двумя числами - числом элементов массива M, больших и меньших Cand.

Это вариация задачи о медиане - "среднем" элементе - массива. Медиану можно определить, например, таким алгоритмом: упорядочив массив, взять элемент, находящийся в середине. Есть и более эффективные алгоритмы. Но я решил ограничиться более простой задачей - проверкой на "медианность". Заметим: если все элементы массива M различны и число их нечетно, то, взяв медиану в качестве Cand, искомая в задаче 10 разность даст значение 0. В общем случае, близость искомой разности к нулю является мерой близости параметра Cand к медиане массива M. Но займемся программистскими аспектами этой задачи. У функции, ее реализующей, на входе - массив, а на выходе - скаляр. Мы хотели бы, чтобы эта функция могла вызываться в формулах рабочего листа, а в качестве фактического параметра ей могли быть переданы как объект Range, так и массив чисел. Вот как я реализовал эту функцию, назвав ее IsMediana:

Public Function IsMediana(M As Variant, Cand As Variant) As Integer 'Дан массив M и элемент Cand. В качестве результата возвращается 'разность между числом элементов массива M, больших и меньших Cand. 'Тем самым можно определить близость Cand к медиане массива M. Dim Pos As Integer, Neg As Integer Pos = 0: Neg = 0 'Анализ типа параметра M If TypeName(M) = "Range" Then For i = 1 To M.Rows.Count For j = 1 To M.Columns.Count If M.Cells(i, j) > Cand Then Pos = Pos + 1 ElseIf M.Cells(i, j) < Cand Then Neg = Neg + 1 End If Next j Next i IsMediana = Pos - Neg

ElseIf TypeName(M) = "Variant()" Then 'TypeName is "Variant()" 'Это массив, но не совсем настоящий, для него не определены, 'например, функции границ: LBound, UBound. Dim Val As Variant For Each Val In M If Val > Cand Then Pos = Pos + 1 ElseIf Val < Cand Then Neg = Neg + 1 End If Next Val IsMediana = Pos - Neg Else MsgBox ("При вызове функции: IsMediana(M,Cand)" & _ vbCrLf & "M не является массивом или объектом Range!") End If

End Function
Прокомментируем работу функции IsMediana.
Функции, чьи аргументы имеют универсальный тип Variant, целесообразно строить по принципу разбора случаев. Алгоритм может изменяться в зависимости от типа фактического параметра, задаваемого в момент вызова.Стандартная функция TypeName(V) возвращает в качестве результата конкретный тип параметра V. Это очень мощная функция VBA, способная разобраться не только с внутренними типами самого языка, но и типами объектов, возвращаемых благодаря Автоматизации (Automation). В частности, функция может определить, имеет ли объект тип Range, File, Sheet или Application.В процессе работы функции IsMediana(M,Cand) разбираются три возможных случая: M - объект Range, M - массив типа Variant, M имеет любой другой тип.В случае, когда функция IsMediana вызывается в формуле рабочего листа Excel, то в качестве фактического параметра ей передается объект Range - интервал ячеек этого листа. Следовательно, функция TypeName возвратит строку "Range" в качестве результата. При обработке этого случая организуется цикл по числу строк и столбцов объекта Range, используя свойство Cells этого объекта.Во втором случае обработка основана на том, что функции передан массив Visual Basic типа Variant. Это возможно, когда при вызове в формуле нашей функции ей передается массив констант. Ниже я приведу примеры подобного вызова. Для таких массивов не определены функции границ UBound и LBound. Поэтому обработка в этом случае основана на использовании цикла For Each.В третьем случае, когда наш параметр не является ни массивом констант, ни объектом Range, в качестве результата по умолчанию выдается 0. Но выдается также и окно сообщений с предупреждением о возникшей ситуации.
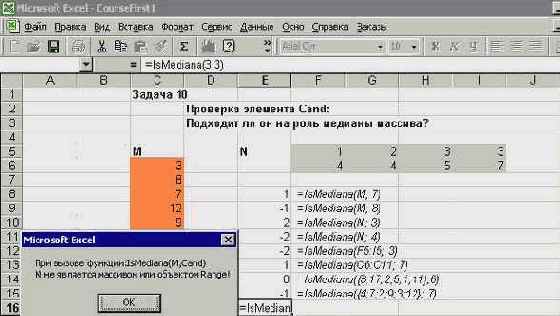
Посмотрим, как это выглядит на экране, и разберем примеры нескольких различных вызовов функции IsMediana в формулах рабочего листа:

увеличить изображение
Рис. 2.5. Вызов функции IsMediana в формулах рабочего листа
На рабочем листе сформированы два массива: вектор M, вытянутый в виде столбца, и прямоугольная матрица N. Вектор M записан в ячейках C6:C11, матрица N - в F5:I6. В ячейки E8:E16 я поместил формулы, вызывающие функцию IsMediana. Они не являются формулами над массивами, несмотря на то, что параметром может быть массив рабочего листа. Важно, что результат - скаляр. Если бы результат, возвращаемый функцией, был массивом, формулу следовало бы вызывать как формулу над массивами. Для скалярного результата это не так.
Хочу обратить внимание на то, что Excel не последователен в этом вопросе. Пользовательская функция, написанная на VBA, аргументы которой являются массивами, но результат которой есть скаляр, может вызываться, как я сказал чуть выше, в обычных формулах рабочего листа. Что касается вызова встроенных функций, то тут ситуация сложнее. Если функции, возвращающей скаляр, передается один массив, то она может вызываться как обычная функция. Если же ей передается несколько массивов, то такой вызов уже должен быть формулой над массивами. Вот классический пример двух вызовов:
=СУММ(A1:D1) {=СУММ(A1:D1 +A2:D2)}

Первый вызов работает нормально, а второй должен быть обязательно формулой над массивами, чтобы результатом действительно была сумма всех элементов двух объектов Range.
Но вернемся к рассмотрению нашей функции IsMediana. В двух первых вызовах функции IsMediana, записанных в ячейках E8, E9, ей передается в качестве параметров имя массива рабочего листа "M" и разные кандидаты: 7 и 8. Они оба годятся на роль медианы этого массива. В следующих двух вызовах проверяются кандидаты на медиану массива N. Как видите, 4 ближе к медиане, чем 3. Следующие два вызова в ячейках E12 и E13 демонстрируют возможность задания диапазона ячеек в момент вызова, что позволяет, например, работать с частью массива. В двух последующих вызовах вообще не используются в качестве входных данных элементы рабочего листа. Входным параметром M является массив констант, заключенный в фигурные скобки, элементы которого разделяются символом ";". В этих случаях фактический параметр уже не является объектом Range, а имеет тип массива с элементами Variant. Поэтому и функция IsMediana будет работать по-другому, в отличие от предыдущих вызовов. Разбор случаев при данном вызове, зависящий от результата, возвращаемого функцией TypeName, приведет к выбору второго варианта. Наконец, вызов, записанный в формуле ячейки E16, демонстрирует случай, когда входной параметр M - обычное число и, следовательно, не является ни объектом Range, ни массивом. Как следствие, разбор случаев в функции IsMediana приводит к третьему варианту и появлению на экране окна сообщений.

Задача 11 Произведение матриц

Постановка задачи: Найти произведение прямоугольных матриц A*B

Из того, что мы узнали ранее, следует, какой вид может иметь заголовок пользовательской функции, решающей эту задачу. Два входных параметра функции должны быть типа Variant. Этот же тип должен быть у возвращаемого функцией значения. Конечно, это не единственно возможное решение. Можно было бы иметь один входной параметр, используя спецификатор ParamArray. Такой способ был бы единственно возможным, если обобщить постановку и попытаться создать функцию, которая должна перемножать произвольное число матриц. Но при умножении двух матриц естественнее иметь и два соответствующих им параметра. Поэтому заголовок получился таким:

Function MultMatr(A As Variant, B As Variant) As Variant

Я хочу показать Вам, как написать общую функцию, достаточно широкого назначения. Ее можно будет вызывать в формулах над массивами рабочего листа, передавая ей в качестве фактических параметров A и B массивы рабочего листа (объекты Range). Но не только объекты Range, но и массивы констант будут допускаться в качестве одного или обоих аргументов. Результат работы функции будет записан в массив, выделенный в момент вызова формулы над массивами. Более того, я хочу, чтобы эту же функцию можно было вызывать в обычных функциях и процедурах VBA, передавая в момент вызова массивы VBA в качестве аргументов. Все это, естественно, утяжелит нашу функцию, но позволит мне обсудить отличия "обычных" и "пользовательских функций. С учетом этих замечаний наша функция выглядит так:

Public Function MultMatr(A As Variant, B As Variant) As Variant 'Умножение матриц. 'Эта функция может вызываться в формулах рабочего листа Excel. 'В этом случае входные параметры являются объектами Range. 'Функцию можно также вызывать в обычных VBA функциях и процедурах, 'передавая ей в качестве параметров массивы VBA.

Dim AB() As Variant Dim i As Integer, j As Integer, k As Integer Dim N As Integer, M As Integer, P As Integer, Q As Integer Dim Correct As Boolean Dim msg1 As String, msg2 As String Dim Elem As Variant Correct = True

'Определение размерностей матриц If TypeName(A) = "Range" Then N = A.Rows.Count: M = A.Columns.Count ElseIf TypeName(A) = "Variant()" Then N = UBound(A, 1): M = UBound(A, 2) Else: Correct = False End If If TypeName(B) = "Range" Then P = B.Rows.Count: Q = B.Columns.Count ElseIf TypeName(A) = "Variant()" Then P = UBound(B, 1): Q = UBound(B, 2) Else: Correct = False End If ' Проверка корректности задания размерности If Correct And (P = M) Then 'Размерность задана корректно ReDim AB(1 To N, 1 To Q) 'Построение произведения матриц AB =A*B For i = 1 To N For j = 1 To Q Elem = 0 For k = 1 To M Elem = Elem + A(i, k) * B(k, j) Next k AB(i, j) = Elem Next j Next i MultMatr = AB Else 'Некорректно заданы аргументы или размерность If Not Correct Then msg2 = " При вызове MultMatr некорректно заданы аргументы!" _ & vbCrLf & "По крайней мере, один из них не является" _ & vbCrLf & "ни массивом, ни объектом Range" MsgBox (msg2) Else msg1 = " При вызове MultMatr некорректно задана размерность" _ & " перемножаемых матриц!" & vbCrLf & _ "Число столбцов в первом сомножителе = " & M & vbCrLf & _ "Число строк второго сомножителя = " & P MsgBox (msg1) End If End If End Function
Сделаем несколько замечаний.
Из-за того, что фактические параметры могут иметь разную природу, приходится анализировать тип параметра, используя уже упоминавшуюся функцию TypeName.В зависимости от того, массивом или объектом Range является параметр, по-разному определяются границы массивов.Если хотя бы один из аргументов не принадлежит ни одному из перечисленных типов, вычисления прерываются с выдачей предупреждающего сообщения.Еще одна проверка, которую я счел обязательной, - проверка на корректность задания размеров перемножаемых матриц. Конечный пользователь может легко ошибиться и не соблюсти обязательное требование при умножении матриц: "число столбцов матрицы A должно совпадать с числом строк матрицы B". В этом случае результат не будет получен, и будет выдано предупреждающее сообщение. Если же пользователь неверно выделит область памяти под результирующую матрицу, вычисления будут идти. Правда, если эта область урезана по отношению к требуемой, часть результатов будет потеряна. Если же область выделена с избытком, выводятся "лишние" результаты, полученные путем копирования.Заметьте, сам процесс вычисления результирующей матрицы выполняется одинаково для обоих типов аргументов.Результат получается в динамическом массиве, который на последнем шаге работы и становится значением функции. Функцию MultMatr я использовал двояко, - вызывая ее в формулах над массивами в рабочем листе Excel и в обычной процедуре VBA, когда мне понадобилось получить произведение двух матриц, представленных обычными массивами VBA.
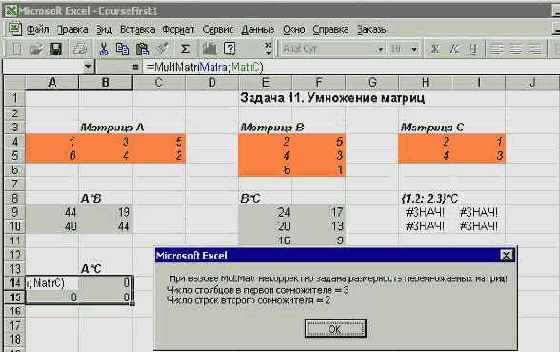
Взгляните, как выглядят результаты некоторых экспериментов по умножению матриц на рабочем листе Excel:

увеличить изображение
Рис. 2.7. Умножение матриц
На рабочем листе я расположил три матрицы разной размерности и дал им имена MatrA, MatrB и MatrC соответственно. Затем, вызывая MultMatr, я получил произведения MatrA*MatrB и MatrB*MatrC, - все выполнилось корректно. Попытка использовать MultMatr для умножения массива констант на матрицу - {1,2; 2,3}*MatrC закончилась неуспехом, поскольку, как я говорил ранее, для массивов констант некорректно работает функция Ubound. При попытке умножения MatrA*MatrC, как и положено, выдалось предупреждающее сообщение о несоблюдении правила размерности перемножаемых матриц.

Задача 12 Решение системы линейных уравнений и обращение матриц

Постановка задачи: Найти решение системы линейных уравнений AX = B

Чтобы одним выстрелом "убить двух зайцев", рассмотрим эту задачу в более общей постановке. Будем полагать, что B - это не вектор правых частей, а матрица из m столбцов, каждый из которых задает правую часть уравнения. Тем самым мы будем решать m систем линейных уравнений с одной и той же левой частью и разными правыми частями. Переход от решения одной системы уравнений к решению m систем сам по себе является важным достоинством рассматриваемого алгоритма. Но более важно то, что здесь же становится возможным находить обратную матрицу для A. Достаточно задать в качестве матрицы правых частей B единичную матрицу E, и тогда матрица X будет обратной к A.

Заголовок функции, решающей эту задачу, имеет такой же вид, как и при умножении матриц и отличается только именем функции:

Function SLEQ(A As Variant, B As Variant) As Variant

Эта функция имеет два входных параметра, - матрицу коэффициентов системы уравнений и матрицу правых частей, и возвращает как результат матрицу X. Конечно, реализация этой функции требует больших усилий, чем умножение матриц. Мне пришлось написать пять процедур, вызываемых в процессе вычислений функции SLEQ. Но сама идея алгоритма достаточно прозрачна. Вначале строится расширенная матрица AB путем присоединения справа матрицы B к матрице A. Затем линейными преобразованиями над ее строками матрица A переводится в единичную матрицу E. Эти же преобразования переводят матрицу B в решение X. Если в качестве B задать единичную матрицу, X будет представлять обратную матрицу. Если B - вектор из одного столбца, то речь идет об обычной системе линейных уравнений. В промежуточном случае B представляет прямоугольную матрицу, и тогда одновременно получа

R± ется решение для m систем линейных уравнений. Теперь приведу текст функции SLEQ и прокомментирую его, а затем уже приведу процедуры, вызываемые по ходу работы. Вот текст основной функции, вызываемой в формуле над массивами рабочего листа Excel:

Public Function SLEQ(A As Variant, B As Variant) As Variant 'Решение системы линейных уравнений: AX = B 'A - матрица коэффициентов, B - матрица правых частей. 'X - матрица решений. 'Для каждого столбца B1 матрицы B соответствующий столбец X1 'является решением системы AX1 = B1. 'Если B - единичная матрица E, то X - матрица, обратная к A. Dim i As Integer, j As Integer Dim N As Integer, M As Integer Dim msg1 As String, msg2 As String msg1 = " При вызове SLEQ система уравнений линейно зависима!" msg2 = " При вызове SLEQ некорректно задана размерность системы уравнений!" 'Проверка корректности задания размерности СЛУР. N = A.Rows.Count If (A.Columns.Count = N) And (B.Rows.Count = N) Then 'Размерность задана корректно. M = B.Columns.Count ReDim AB(1 To N, 1 To N + M) 'Построение расширенной матрицы. For i = 1 To N For j = 1 To N AB(i, j) = A.Cells(i, j) Next j Next i For i = 1 To N For j = 1 To M AB(i, N + j) = B.Cells(i, j) Next j Next i 'Цикл линейных преобразований над матрицей AB. Dim k As Integer Dim Independence As Boolean k = 1: Independence = True Do Independence = FindMax(AB, k, i) If Not Independence Then Exit Do Call Change(AB, k, i) Call Normalization(AB, k) Call Linear(AB, k) k = k + 1 Loop While k <= N If Not Independence Then MsgBox (msg1)

Постановка задачи: Найти решение системы линейных уравнений AX = B
Чтобы одним выстрелом "убить двух зайцев", рассмотрим эту задачу в более общей постановке. Будем полагать, что B - это не вектор правых частей, а матрица из m столбцов, каждый из которых задает правую часть уравнения. Тем самым мы будем решать m систем линейных уравнений с одной и той же левой частью и разными правыми частями. Переход от решения одной системы уравнений к решению m систем сам по себе является важным достоинством рассматриваемого алгоритма. Но более важно то, что здесь же становится возможным находить обратную матрицу для A. Достаточно задать в качестве матрицы правых частей B единичную матрицу E, и тогда матрица X будет обратной к A.
Заголовок функции, решающей эту задачу, имеет такой же вид, как и при умножении матриц и отличается только именем функции:
Function SLEQ(A As Variant, B As Variant) As Variant
Эта функция имеет два входных параметра, - матрицу коэффициентов системы уравнений и матрицу правых частей, и возвращает как результат матрицу X. Конечно, реализация этой функции требует больших усилий, чем умножение матриц. Мне пришлось написать пять процедур, вызываемых в процессе вычислений функции SLEQ. Но сама идея алгоритма достаточно прозрачна. Вначале строится расширенная матрица AB путем присоединения справа матрицы B к матрице A. Затем линейными преобразованиями над ее строками матрица A переводится в единичную матрицу E. Эти же преобразования переводят матрицу B в решение X. Если в качестве B задать единичную матрицу, X будет представлять обратную матрицу. Если B - вектор из одного столбца, то речь идет об обычной системе линейных уравнений. В промежуточном случае B представляет прямоугольную матрицу, и тогда одновременно получа
R± ется решение для m систем линейных уравнений. Теперь приведу текст функции SLEQ и прокомментирую его, а затем уже приведу процедуры, вызываемые по ходу работы. Вот текст основной функции, вызываемой в формуле над массивами рабочего листа Excel:
Public Function SLEQ(A As Variant, B As Variant) As Variant 'Решение системы линейных уравнений: AX = B 'A - матрица коэффициентов, B - матрица правых частей. 'X - матрица решений. 'Для каждого столбца B1 матрицы B соответствующий столбец X1 'является решением системы AX1 = B1. 'Если B - единичная матрица E, то X - матрица, обратная к A. Dim i As Integer, j As Integer Dim N As Integer, M As Integer Dim msg1 As String, msg2 As String msg1 = " При вызове SLEQ система уравнений линейно зависима!" msg2 = " При вызове SLEQ некорректно задана размерность системы уравнений!" 'Проверка корректности задания размерности СЛУР. N = A.Rows.Count If (A.Columns.Count = N) And (B.Rows.Count = N) Then 'Размерность задана корректно. M = B.Columns.Count ReDim AB(1 To N, 1 To N + M) 'Построение расширенной матрицы. For i = 1 To N For j = 1 To N AB(i, j) = A.Cells(i, j) Next j Next i For i = 1 To N For j = 1 To M AB(i, N + j) = B.Cells(i, j) Next j Next i 'Цикл линейных преобразований над матрицей AB. Dim k As Integer Dim Independence As Boolean k = 1: Independence = True Do Independence = FindMax(AB, k, i) If Not Independence Then Exit Do Call Change(AB, k, i) Call Normalization(AB, k) Call Linear(AB, k) k = k + 1 Loop While k <= N If Not Independence Then MsgBox (msg1)

'Возвращение результата. For i = 1 To N For j = 1 To M AB(i, j) = AB(i, j + N) Next j Next i ReDim Preserve AB(1 To N, 1 To M) SLEQ = AB Else 'Некорректно задана размерность. MsgBox (msg2) End If
End Function
Дам теперь необходимые пояснения:
В реализации функции можно выделить три основные части: построение расширенной матрицы, цикл линейных преобразований и формирование результирующей матрицы. Для построения расширенной матрицы вводится динамический массив AB. Его заполнение достаточно очевидно. Окончательный результат представляет лишь часть расширенной матрицы и формируется на месте исходной матрицы B. Чтобы выделить эту часть, я использую возможности динамического массива: переопределяю его размерность и затем, используя спецификатор Preserve, сохраняю нужные результаты. Таким образом, новый массив не вводится, а сжимается существующий до нужного размера. Правда, это сжатие возможно лишь для последнего измерения. Поэтому предварительно нужные результаты переписываются в начало массива AB.С содержательной точки зрения основу алгоритма составляет цикл, в котором над матрицей выполняются линейные преобразования. Алгоритм реализует схему Гаусса с выбором главного элемента в столбце. На каждом шаге цикла линейными преобразованиями над строками матрицы ее очередной k-й столбец приводится к единичному столбцу с единицей на диагонали матрицы и остальными нулевыми элементами. Вначале вызывается функция FindMax, которая в k-ом столбце находит максимальный по модулю элемент, расположенный ниже диагонали. Процедура Change меняет строки местами, так чтобы найденный максимальный элемент стал диагональным. Процедура Normalization нормирует k-ю строку делением всех ее элементов на элемент, расположенный на диагонали. Сам этот элемент тем самым становится равным 1. Процедура Linear выполняет линейные преобразования над строками, вычитая из каждой строки k-ю строку, умноженную на подходящий коэффициент, так чтобы сделать нулевыми все элементы k-го столбца, расположенные выше и ниже диагонали.Вначале проверяется корректность задания размерности матриц A и B. Подобная проверка проводилась при умножении матриц. Вторая проверка позволяет обнаружить линейную зависимость строк или столбцов матрицы A. В случае линейной зависимости система уравнений не имеет единственного решения, а обратную матрицу вычислить невозможно.Данная функция является чисто пользовательской, и я ориентируюсь лишь на один способ передачи параметров, - в виде Range-объектов.

Приведу теперь тексты процедур, вызываемых в теле функции SLEQ, и начну с функции FindMax:
Public Function FindMax(A() As Variant, ByVal Num As Integer, _ Ind As Integer) As Boolean 'В столбце с номером Num матрицы A, начиная с диагонального элемента, 'ищется максимальный по абсолютной величине элемент, 'и вычисляется его индекс Ind. 'Функция возвращает true, если элемент отличен от нуля. Dim i As Integer, Elem As Variant Elem = Abs(A(Num, Num)): Ind = Num For i = Num + 1 To UBound(A, 1) If Abs(A(i, Num)) > Elem Then Elem = Abs(A(i, Num)): Ind = i End If Next i FindMax = Not (Elem = 0)
End Function
Прежде всего, заметьте, что в теле пользовательской функции SLEQ вызываются обычные процедуры и функции. Помимо своей основной задачи - нахождения максимального по модулю элемента столбца и определения его индекса Ind, -булева функция FindMax позволяет определить, является ли система уравнений линейно зависимой. Если найденный элемент равен 0, то и все остальные элементы равны 0, а это и есть признак линейной зависимости. Эта проверка предохраняет нас от возможного деления на 0. Конечно, разумнее выполнять не строгую, а слабую проверку на 0, полагая, что система "почти линейно зависима" (плохо обусловлена), если вычисляемый нами элемент близок к 0. Но это уже вычислительные, а не программистские аспекты, которые здесь обсуждать не место. Следующие две процедуры Change и Normalization совсем простые:
Public Sub Change(A() As Variant, _ ByVal Ind1 As Integer, ByVal Ind2 As Integer) 'Перестановка строк с индексами Ind1 и Ind2 матрицы A Dim i As Integer, Elem As Variant If Not (Ind1 = Ind2) Then For i = LBound(A, 2) To UBound(A, 2) Elem = A(Ind1, i) A(Ind1, i) = A(Ind2, i) A(Ind2, i) = Elem Next i End If End Sub
Public Sub Normalization(A() As Variant, Ind As Integer) 'Нормировка строки с индексом Ind матрицы A 'делением на диагональный элемент. Dim i As Integer, Elem As Variant Elem = A(Ind, Ind): A(Ind, Ind) = 1 For i = Ind + 1 To UBound(A, 2) A(Ind, i) = A(Ind, i) / Elem Next i

Постановка задачи: Используя Решатель, найти

Постановка задачи: Используя Решатель, найти решение уравнения: F(x) = a*x^4 + b*x^3 + c*x^2 + d*x + e =0,
В задачах 3 и 4 предыдущей главы для нахождения корней этого уравнения я применил метод Ньютона, и сам определял процесс построения решения. Покажу теперь, как воспользоваться Решателем. Наша задача без труда укладывается в общую постановку. Целевая функция - уравнение F(x). Требуется найти такое значение регулируемой ячейки x, чтобы функция F(x) приняла фиксированное значение, равное 0. Никаких ограничений на переменную x не накладывается. Так что все, что нужно, - записать в одну из ячеек рабочего листа переменную x, в другую - формулу, задающую функцию F(x), и вызвать Solver (Решатель) из меню Сервис. Вот как это выглядит на рабочем листе:

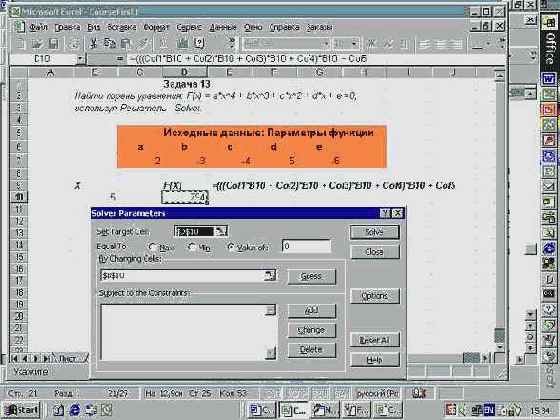
увеличить изображение
Рис. 2.9. Вызов Решателя для поиска корней нелинейного уравнения
Как видите, в диалоговом окне Решателя:
в окне "Установить ячейку цели" (Set Target Cell) задана ссылка на ячейку, содержащую формулу для вычисления значения функции F(x);включен переключатель "Значение" (Value of) и задано значение 0 в его окошке;в окне регулируемых ячеек (By Changing Cells) задана ссылка на ячейку, содержащую x; кстати, можно щелкнуть командную кнопку "Догадка" (Guess), и Решатель автоматически попытается сформировать весь список регулируемых ячеек, от которых зависит целевая функция;так как в нашем случае ограничений задавать не нужно, то больше ничего делать не нужно и можно запустить процесс поиска решения щелчком командной кнопки "Решение" (Solve).
Полученное решение зависит от выбора начального приближения, которое задается в ячейке x перед обращением к Решателю. Вот так выглядит окно Решателя при успешном завершении поиска решения:

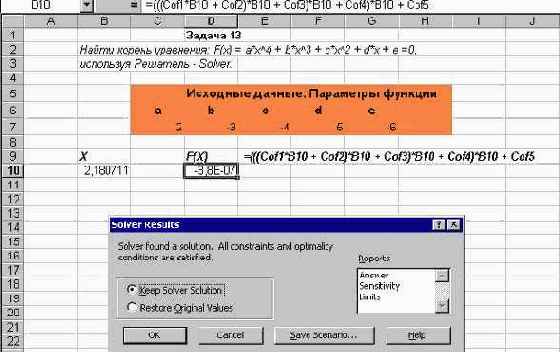
увеличить изображение
Рис. 2.10. Окно Решателя при успешном поиске решения
Наряду с появлением уведомления об успехе поиска в окне "Отчеты" (Reports) предлагается выбрать любые из трех возможных отчетов по результатам работы. Кроме того, можно сохранить полученные результаты или восстановить первоначальные значения. Можно также запомнить созданную постановку задачи. Вот как выглядит отчет "Результаты" (Answer) в нашем случае:

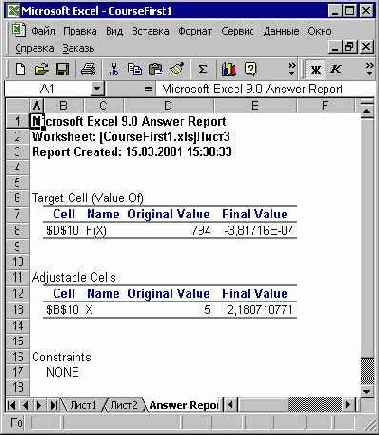
Рис. 2.11. Отчет "Результаты", уведомляющий о результатах решения

Постановка задачи: Используя Решатель, найти

Постановка задачи: Используя Решатель, найти решение системы линейных уравнений AX = B
Решение системы уравнений как линейных, так и нелинейных нетрудно сформулировать как оптимизационную задачу в постановке, требуемой Решателем. Пусть имеется система уравнений:
F1(X) = 0; F2(X) = 0; … Fn(X) = 0;
Для Решателя эта задача естественным образом формулируется так:
вектор переменных X представляет массив регулируемых ячеек;функции FI(X) задают ограничения типа равенств;в качестве целевой функции можно выбрать, например, Ф(X) = SUM(FI(X)). При этом можно выбирать любой критерий для целевой функции, устремляя ее к минимуму, максимуму или требуя нулевое значение для Ф(X).
В качестве примера я использовал те же данные, что и в задаче 12. Взгляните, как выглядит постановка этой задачи в окне Решателя:

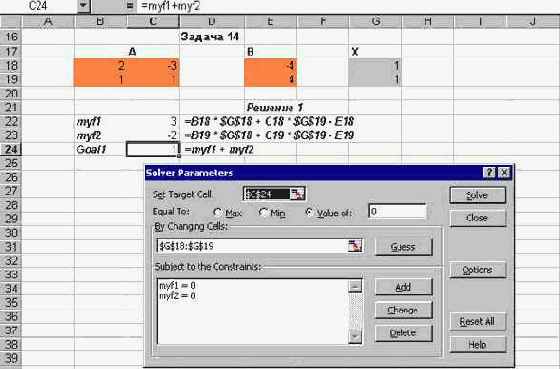
увеличить изображение
Рис. 2.14. Постановка задачи в окне Решателя
А вот как выглядит решение, найденное Решателем:

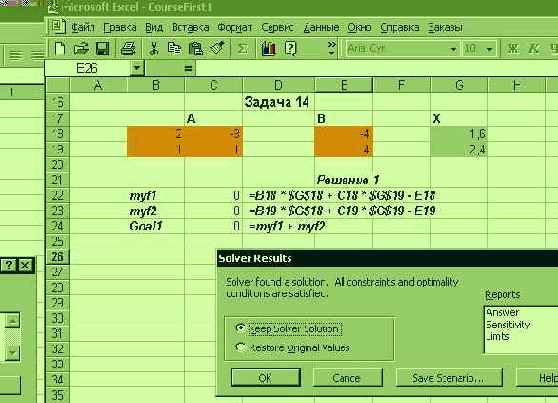
Рис. 2.15. Решение системы линейных уравнений, найденное Решателем

Постановка задачи: Используя Решатель, найти решение системы линейных уравнений AX = B
Решение системы уравнений как линейных, так и нелинейных нетрудно сформулировать как оптимизационную задачу в постановке, требуемой Решателем. Пусть имеется система уравнений:
F1(X) = 0; F2(X) = 0; … Fn(X) = 0;
Для Решателя эта задача естественным образом формулируется так:
вектор переменных X представляет массив регулируемых ячеек;функции FI(X) задают ограничения типа равенств;в качестве целевой функции можно выбрать, например, Ф(X) = SUM(FI(X)). При этом можно выбирать любой критерий для целевой функции, устремляя ее к минимуму, максимуму или требуя нулевое значение для Ф(X).
В качестве примера я использовал те же данные, что и в задаче 12. Взгляните, как выглядит постановка этой задачи в окне Решателя:

Рис. 2.15. Решение системы линейных уравнений, найденное Решателем
Нужно понимать, что когда используется Решатель, многое зависит еще и от того, как сформулирована задача. Решатель допускает различные постановки одной и той же задачи, а также имеет ряд параметров, позволяющих управлять процессом решения. Так, при решении системы линейных уравнений можно, например, рассматривать задачу как задачу минимизации следующей функции:
Ф(X) = F12 (X) + F22 (X) + … +Fn2 (X) -> Min
При минимизации этой функции можно и не задавать ограничения. Понятно, что решение системы исходных уравнений является точкой минимума целевой функции Ф(X). На следующих рисунках показана постановка задачи и ее решение для этого варианта постановки:

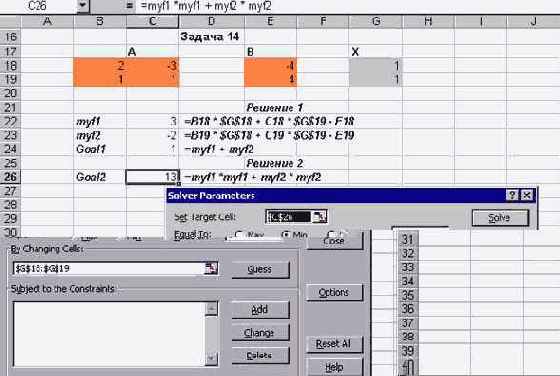
увеличить изображение
Рис. 2.16. Второй вариант постановки задачи

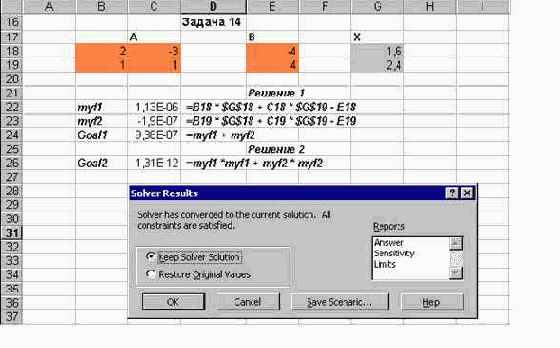
увеличить изображение
Рис. 2.17. Решение, найденное Решателем, во втором варианте
Как видите, в обеих постановках Решатель успешно находит решение системы линейных уравнений. Чтобы убедиться, что "проклятие размерности" не так уж и страшно Решателю, я провел еще один эксперимент, выбрав задачу большей размерности, и стал искать решение системы из пяти линейных уравнений. На рабочем листе Excel я задал:
матрицу коэффициентов этой системы - myA;вектор правых частей - myB;вектор переменных - SolX5в ячейках Myl1-Myl5 формулы, задающие соответствующие линейные уравнения. Фактически, я ввел одну формулу в ячейку myl1: {=СУММ(B30:F30*SolX5) -I30}

Затем скопировал ее в соседние ячейки. При копировании автоматически изменяется диапазон ячеек, который указывает на следующую строку матрицы коэффициентов, и изменяется ссылка на ячейку, задающую правую часть уравнения.
В ячейки с именами MYST и MYST1 я ввел формулы для целевых функций, соответствующих двум различным постановкам: =Myl1 + Myl2 + Myl3 + Myl4 + Myl5; = Myl1* Myl1 + Myl2* Myl2 + Myl3* Myl3 + Myl4* Myl4 + Myl5* Myl5;В первом случае целевая функция линейна, но задаются дополнительные ограничения. Во втором - минимизируется квадратичная функция при отсутствии ограничений. Диалоговое окно Решателя в момент задания его параметров при оптимизации первой целевой функции выглядит так:

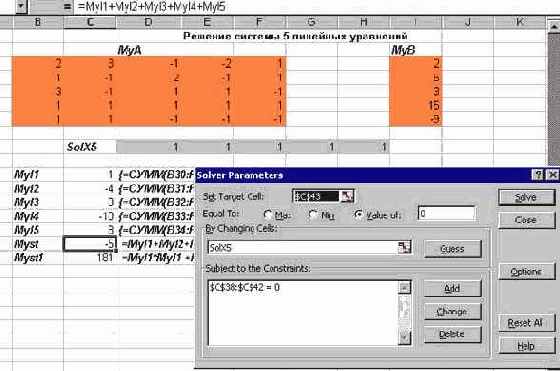
увеличить изображение
Рис. 2.18. Постановка задачи линейного программирования
Обратите внимание на некоторые детали постановки задачи. В окне изменяемых ячеек я задал имя вектора решений - SolX5. Вектор ограничений распространяется на весь диапазон уравнений, но формально задан в виде одного векторного ограничения. Перед тем, как приступить к решению, я изменил настройку параметров Решателя. Взгляните, как выглядит окно Options (Параметры), в котором производится настройка:

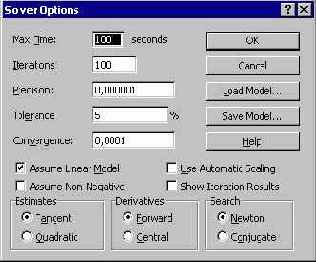
Рис. 2.19. Настройка параметров Решателя
Как видите, возможностей управлять решением достаточно много, и я еще позже поговорю о них подробнее. Сейчас же замечу, что я оставил без изменения максимальное время, отводимое на решение - 100 секунд, максимальное число итераций - 100, требуемую точность выполнения ограничений - 0, 0000001. Единственное, что я сделал, это включил флажок Linear, указав, что в данной постановке Решатель имеет дело с задачей линейного программирования, поскольку все ограничения и целевая функция линейно зависят от переменных задачи.
Точное решение нашей системы уравнений задается вектором (1, 2, 3, 4, 5). Решатель нашел это решение.

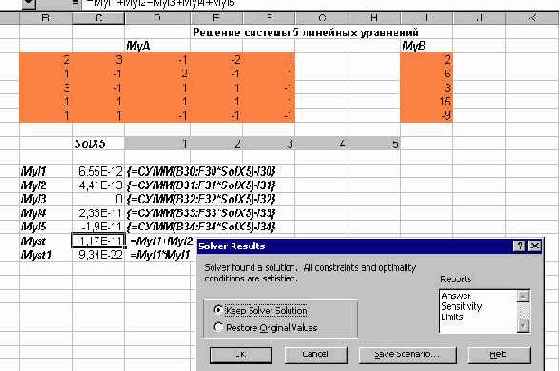
увеличить изображение
Рис. 2.20. Решение системы 5 линейных уравнений с линейной целевой функцией
Я получил также решение этой задачи и для квадратичной целевой функции в различных постановках: с учетом ограничений, без их учета, минимизируя или требуя, чтобы функция принимала нулевое решение. Во всех случаях, поверьте, Решатель не подкачал.

Задача о краске

Мне нравится рассказывать об этой задаче, которая принадлежит В. Очкову, и взята "из жизни" в период середины 90-х годов, когда бартер играл основную роль при расчетах. С тех пор ситуация в экономике существенно изменилась в лучшую сторону, хотя до нормы еще далеко. При описании содержательной постановки я хочу сохранить весь внешний "антураж". Заметьте, цены в те годы примерно на 4 порядка отличались от нынешних. Суть задачи такова. Коллектив программистов под руководством В. Очкова написал программу и продал ее за 14 миллионов лакокрасочному предприятию. "Живых" денег предприятие не платило, но могло в пределах указанной суммы расплатиться краской - своей продукцией. Институт, в котором работал В. Очков, нуждался в краске и готов был оплатить привезенную краску. Краска выпускалась в двух видах тары - больших и малых банках (барабанах), емкость которых составляла 55 и 15 литров, а стоимость пустых барабанов составляла - 30 и 24 тысячи рублей. Литр краски стоит 14 600 рублей. Спрашивается, сколько больших и сколько малых барабанов следует взять, если учесть, что институт заинтересован получить как можно больше краски, а создатель программы скорее заинтересован в том, чтобы как можно меньше денег оставить "лакокрасочникам". Типичная оптимизационная задача!

Для решения этой задачи (кстати, это задача с целочисленными переменными) автор использовал Решатель. Благо Excel уже тогда можно было найти повсюду, в том числе и в бухгалтерии лакокрасочного завода. В поставленной Решателю задаче требовалось максимизировать объем получаемой краски при естественном ограничении на сумму имеющихся денег и ограничений целочисленности на искомые переменные - число больших и малых барабанов. Используя установки параметров, принятые по умолчанию, найденный Решателем "оптимальный" ответ гласил, следует взять 2 малых и 16 больших барабанов с краской. Это давало 910 литров краски, но оставляло предприятию 186000 рублей. Возможно, остаток денег был большой, но В. Очков не поверил Решателю и стал искать другой ответ. И нашел лучшее решение. Оно таково: следует взять 15 больших и 6 малых барабанов. При этом краски будет больше (915 л), а денег, заработанных автором, у завода останется значительно меньше (47 000 руб.). Надеюсь, Вы понимаете, что второе решение было получено за счет разумного управления параметрами Решателя. Я напомню, что когда решается задача с целочисленными ограничениями на переменные, вначале ищется решение без учета таких ограничений. Здесь такое оптимальное решение можно найти самому, поскольку понятно, что максимизации объема можно добиться, закупая краску в больших банках. Наша сумма денег позволяет взять примерно 16,8 больших барабанов, т. е. около 924 л. Но брать неполные банки нельзя и, следовательно, нужно искать целочисленное значение. В окрестности найденного оптимального решения Решатель ищет ближайшую целочисленную точку. Значение целевой функции в ней не должно отличаться более чем на величину, заданную параметром Tolerance. Напомним, по умолчанию это значение равно 5%, что в данном примере немало: 46,2 л. Первое решение, выданное Решателем, вполне укладывается в допустимые рамки. Если уменьшить значение параметра Tolerance до 1%, Решатель найдет другое, действительно оптимальное целочисленное решение.

История с "оптимальными" решениями имеет продолжение. Рассмотрим еще одно решение с другой целевой функцией, в котором минимизировалась сумма денег, оставляемая заводу. В этом решении следует взять 37 малых и только 6 больших барабанов. Тогда заводу останется только 11 000 руб., так что краска будет закуплена почти на все заработанные автором деньги. Правда, краски будет меньше, - всего 885 литров. Но! Когда это решение было показано тем, кому предназначалась краска, они также признали его наилучшим. С большими барабанами больше возни, и краски на переливах из большого барабана теряется больше. Если ввести дополнительные ограничения на потери, то нормальное решение 37 и 6 может быть получено и при максимизации объема закупаемой краски. Обратите внимание, как, решая, по сути, одну и ту же оптимизационную задачу, можно найти принципиально разные решения. Многое зависит от удачной постановки, выбора критериев, ограничений. Немаловажное значение имеет и умение управлять параметрами алгоритмов оптимизации.

Давайте и мы решим эту задачу. Приведу два решения с различными целевыми функциями. Я не буду подробно рассказывать, в какие ячейки помещаются исходные данные, какие формулы записаны в ячейках. Все это, как и результаты, показано на рисунке:

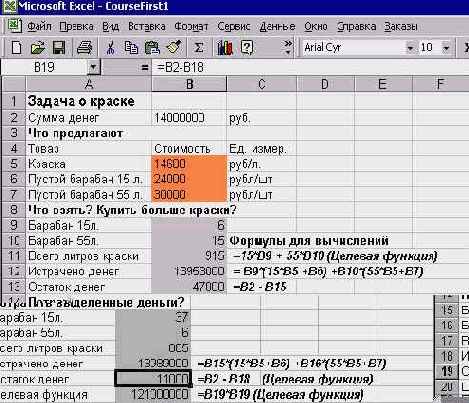
Рис. 2.24. Две постановки и два решения задачи о красках

В первой постановке этой задачи максимизируется объем закупаемой краски при ограничении на сумму истраченных денег и требовании целочисленности искомых переменных. Во второй постановке минимизировалась сумма денег, оставляемая заводу. В качестве целевой функции можно выбирать функцию, задающую остаток денег, или рассматривать квадратичную целевую функцию. Ограничения на положительность переменных, их целочисленность и на остаток денег во всех случаях одни и те же. Вот как выглядит окно Решателя в момент постановки задачи, когда минимизируется остаток денег:

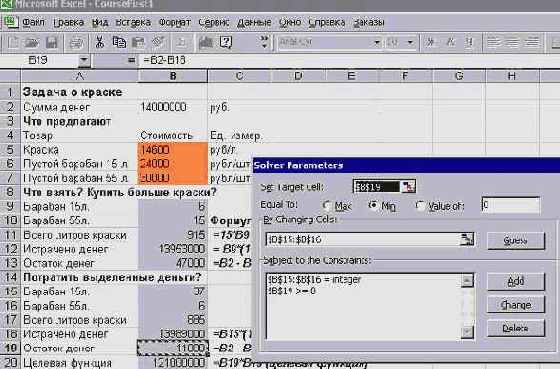
увеличить изображение
Рис. 2.25. Минимизация остатка денег

Задачи с массивами и программирование

Я хочу теперь сосредоточиться на программном решении классических задач математики, возникающих при обучении программистов. Большинство задач, требующих выполнения операций над матрицами, без программирования не решить. Вместе с тем, библиотека встроенных функций включает основные операции - транспонирование матрицы, умножение и обращение матриц. Для обучения всегда полезно уметь написать собственную реализацию встроенных функций, чем мы сейчас и займемся.